题目内容
19．已知集合A={x|1＜x-1≤4}，B=（-∞，a），若A⊆B，则实数a的取值范围是（5，+∞）．分析 先解出集合A=（2，5]，而根据A⊆B便得到，a＞5，即可得出结论．
解答 解：A=（2，5]，A⊆B；
∴5＜a，
∴a∈（5，+∞）．
故答案为：（5，+∞）．
点评 考查子集的概念，注意由A⊆B得到5＜a，而不是5≤a．
练习册系列答案
备战中考寒假系列答案
相关题目
9．已知-1＜α＜0，则（ ）
| A． | ${0.2^α}＞{（\frac{1}{2}）^α}＞{2^α}$ | B． | ${2^α}＞{0.2^α}＞{（\frac{1}{2}）^α}$ | C． | ${（\frac{1}{2}）^α}＞{0.2^α}＞{2^α}$ | D． | ${2^α}＞{（\frac{1}{2}）^α}＞{0.2^α}$ |
14．已知等比数列{an}的前n项和为Sn，则下列一定成立的是（ ）
| A． | 若a3＞0，则a2015＜0 | B． | 若a4＞0，则a2015＜0 | ||
| C． | 若a3＞0，则a2015＞0 | D． | 若a4＞0，则a2015＞0 |
4．已知焦点在y轴上的椭圆方程为$\frac{x^2}{6-m}+\frac{y^2}{m-4}=1$，则m的范围为（ ）
| A． | （4，6） | B． | （5，6） | C． | （6，+∞） | D． | （-∞，4） |
11．
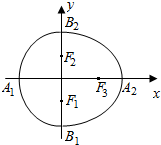我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x≥0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角形，则a，b的值分别为（ ）
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x≥0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角形，则a，b的值分别为（ ）| A． | 5，4 | B． | $\sqrt{3}$，1 | C． | 5，3 | D． | $\frac{\sqrt{7}}{2}$，1 |
8．已知函数f（x）=$\frac{1}{3}$sin（ωx+$\frac{π}{3}$）（ω＞0）的最小正周期为π，则f（x）的图象（ ）
| A． | 关于直线x=$\frac{π}{4}$对称 | B． | 关于点（$\frac{π}{4}$，0）对称 | ||
| C． | 关于直线x=$\frac{π}{3}$对称 | D． | 关于点（$\frac{π}{3}$，0）对称 |