题目内容
4.已知函数f(x)=2-x2-log2x,正实数a、b、c满足f(a)<f(b)<0<f(c),若实数m是方程f(x)=0的一个根,那么下列四个结论:①m>a;②m<b;③m>c;④$m>\frac{1}{2}(a+b)$.其中成立的是②③.分析 先求函数f(x)的定义域,再判断f(x)=2-x2-log2x在(0,+∞)上是减函数;从而可得a>b>m>c;从而解得.
解答 解:∵f(x)=2-x2-log2x的定义域为(0,+∞),
又∵y=2-x2在(0,+∞)上是减函数,
y=-log2x在(0,+∞)上是减函数,
∴f(x)=2-x2-log2x在(0,+∞)上是减函数;
又∵实数m是方程f(x)=0的一个根,
∴f(m)=0,
∴f(a)<f(b)<f(m)<f(c),
∴a>b>m>c;
∴m<a,m<b,m>c,m<$\frac{1}{2}$(a+b);
故答案为:②③.
点评 本题考查了函数的单调性的判断与应用,同时考查了方程的根与函数零点的关系应用,属于中档题.

练习册系列答案
相关题目
12.直线l过点(2,3)且与直线m:3x+2y-4=0垂直,则直线l的方程为( )
| A. | 3x+2y-12=0 | B. | 2x+3y-13=0 | C. | 3x-2y=0 | D. | 2x-3y+5=0 |
9.用火柴棒摆“金鱼”,如图所示:
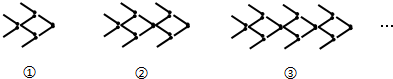
按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )

按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )
| A. | 58 | B. | 78 | C. | 62 | D. | 82 |
16.若$\overrightarrow a=(2x,1,3),\overrightarrow b=(1,-2y,9)$,若$\overrightarrow a$∥$\overrightarrow b$,则( )
| A. | x=1,y=1 | B. | $x=\frac{1}{2},y=-\frac{1}{2}$ | C. | $x=\frac{1}{6},y=-\frac{3}{2}$ | D. | $x=-\frac{1}{6},y=\frac{3}{2}$ |
13.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1,F2,椭圆上存在点P,使得∠F1PF2=60°,则椭圆的离心率的取值范围是( )
| A. | $({0,\frac{1}{2}}]$ | B. | $[{\frac{1}{2},1})$ | C. | $({0,\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{{\sqrt{3}}}{2},1})$ |