题目内容
13.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1,F2,椭圆上存在点P,使得∠F1PF2=60°,则椭圆的离心率的取值范围是( )| A. | $({0,\frac{1}{2}}]$ | B. | $[{\frac{1}{2},1})$ | C. | $({0,\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{{\sqrt{3}}}{2},1})$ |
分析 当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时,P对两个焦点的张角∠F1PF2渐渐增大,当且仅当P点位于短轴端点P0处时,张角∠F1PF2达到最大值,由此可得结论.
解答 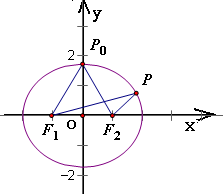 解:如图,当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时,P对两个焦点的张角∠F1PF2渐渐增大,当且仅当P点位于短轴端点P0处时,张角∠F1PF2达到最大值.由此可得:
解:如图,当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时,P对两个焦点的张角∠F1PF2渐渐增大,当且仅当P点位于短轴端点P0处时,张角∠F1PF2达到最大值.由此可得:
∵存在点P为椭圆上一点,使得∠F1PF2=60°,
∴△P0F1F2中,∠F1P0F2≥60°,
∴Rt△P0OF2中,∠OP0F2≥30°,
所以P0O≤$\sqrt{3}$OF2,即b≤$\sqrt{3}$c,
∴a2-c2≤3c2,可得a2≤4c2,
∴$\frac{c}{a}$≥$\frac{1}{2}$,
∵0<e<1,
∴$\frac{1}{2}≤e<1$.
故选:B.
点评 本题考查了直角三角形的三角函数和椭圆的简单几何性质等知识点,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
8.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1,F2,过右焦点F2作x轴的垂线,交椭圆于A,B两点.若等边△ABF1的周长为$4\sqrt{3}$,则椭圆的方程为( )
| A. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | B. | $\frac{x^2}{3}+\frac{y^2}{6}=1$ | C. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ |
18.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x(x<0)}\\{\frac{ln(x+1)}{x+1},(x≥0)}\end{array}\right.$,参数k∈[-1,1],则方程f(x)-kx-k=0有四个实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2e}$ | D. | $\frac{1}{4e}$ |
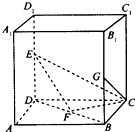 如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.