题目内容
已知f(x)是偶函数,且f(x)在[0,+∞)上是增函数,若x∈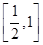 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
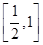 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.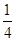 ≤a≤1
≤a≤1∵f(x)是偶函数,当x∈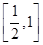 时,不等式f(1+xlog2a)≤f(x-2)等价于f(|1+xlog2a|)≤f(2-x).
时,不等式f(1+xlog2a)≤f(x-2)等价于f(|1+xlog2a|)≤f(2-x).
又f(x)在[0,+∞)上是增函数,∴|1+xlog2a|≤2-x,
∴x-2≤1+xlog2a≤2-x,∴1-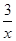 ≤log2a≤
≤log2a≤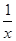 -1,
-1,
上述不等式在x∈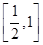 上恒成立,∴
上恒成立,∴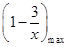 ≤log2a≤
≤log2a≤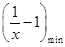 ,
,
∴-2≤log2a≤0,解得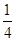 ≤a≤1.
≤a≤1.
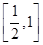 时,不等式f(1+xlog2a)≤f(x-2)等价于f(|1+xlog2a|)≤f(2-x).
时,不等式f(1+xlog2a)≤f(x-2)等价于f(|1+xlog2a|)≤f(2-x).又f(x)在[0,+∞)上是增函数,∴|1+xlog2a|≤2-x,
∴x-2≤1+xlog2a≤2-x,∴1-
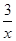 ≤log2a≤
≤log2a≤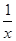 -1,
-1,上述不等式在x∈
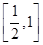 上恒成立,∴
上恒成立,∴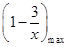 ≤log2a≤
≤log2a≤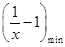 ,
,∴-2≤log2a≤0,解得
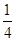 ≤a≤1.
≤a≤1.
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
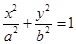 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q). 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程. 对任意实数
对任意实数 恒有
恒有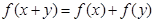 且当
且当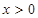 时,有
时,有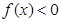 且
且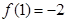 .
. 上的最大值;
上的最大值;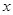 的不等式
的不等式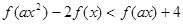 .
.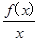 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.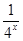 -
-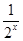 +1的最小值与最大值.
+1的最小值与最大值.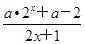 (x∈R),试确定a的值,使f(x)为奇函数;
(x∈R),试确定a的值,使f(x)为奇函数;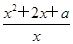 ,x∈[1,+∞).
,x∈[1,+∞).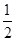 时,求f(x)的最小值;
时,求f(x)的最小值; (x≠0,a∈R).
(x≠0,a∈R).