题目内容
已知椭圆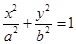 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(1).当p+q≤0时,求椭圆的离心率的取值范围;
(2).若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时, 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.
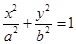 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).(1).当p+q≤0时,求椭圆的离心率的取值范围;
(2).若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时,
 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.(1) ;(2)
;(2)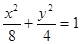 .
.
 ;(2)
;(2)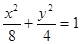 .
.试题分析:本题主要考查直线和圆的方程、椭圆的方程、离心率、向量的运算、二次函数的最值等基础知识,意在考查考生的运算求解能力、推理论证能力以及利用函数与方程思想、数形结合思想的解题能力.
第一问,利用AF、AB的中垂线的交点为圆心,得到圆心坐标,由已知令
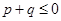 ,解出a,c的关系,从而求离心率e的范围;第二问,结合第一问得
,解出a,c的关系,从而求离心率e的范围;第二问,结合第一问得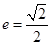 ,则得出基本量a,b,c的关系,设出椭圆方程,用c表示,并确定点M的横坐标的取值范围,利用向量的数量积,得出关于x的表达式,利用配方法,通过讨论抛物线的对称轴
,则得出基本量a,b,c的关系,设出椭圆方程,用c表示,并确定点M的横坐标的取值范围,利用向量的数量积,得出关于x的表达式,利用配方法,通过讨论抛物线的对称轴 与
与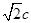 的大小来决定最小值在哪个位置取得,令最小值等于
的大小来决定最小值在哪个位置取得,令最小值等于 ,解出c的值,从而确定椭圆的标准方程.
,解出c的值,从而确定椭圆的标准方程.试题解析:(1)设半焦距为
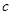 .由题意
.由题意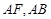 的中垂线方程分别为
的中垂线方程分别为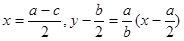 ,
,于是圆心坐标为
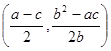 .所以
.所以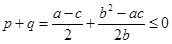 ,
,整理得
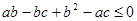 , 4分
, 4分即
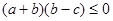 ,
,所以
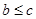 ,于是
,于是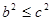 ,即
,即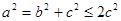 .
.所以
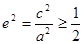 ,即
,即 . 6分
. 6分(2)当
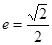 时,
时,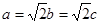 ,此时椭圆的方程为
,此时椭圆的方程为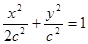 ,
,设
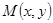 ,则
,则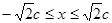 ,
,所以
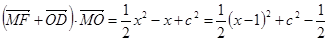 . 8分
. 8分当
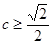 时,上式的最小值为
时,上式的最小值为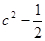 ,即
,即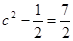 ,得
,得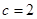 ; 10分
; 10分当
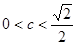 时,上式的最小值为
时,上式的最小值为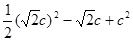 ,即
,即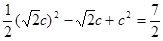 ,
,解得
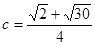 ,不合题意,舍去.
,不合题意,舍去.综上所述,椭圆的方程为
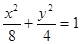 . 12分
. 12分
练习册系列答案
相关题目
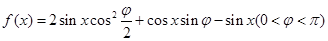 ,在
,在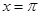 处取最小值.
处取最小值.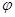 的值;
的值;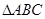 中,
中,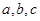 分别是
分别是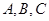 的对边,已知
的对边,已知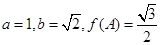 ,求角
,求角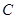 .
.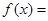
 则满足
则满足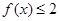 的
的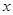 的取值范围是 .
的取值范围是 .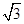 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )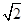
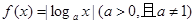 的单调递增区间是 .
的单调递增区间是 .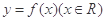 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有 .当
.当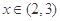 时,
时,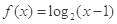 ,给出以下4个结论:①函数
,给出以下4个结论:①函数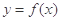 的图象关于点(k,0)(k
的图象关于点(k,0)(k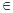 Z)成中心对称;②函数
Z)成中心对称;②函数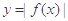 是以2为周期的周期函数;③当
是以2为周期的周期函数;③当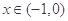 时,
时,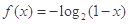 ;④函数
;④函数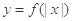 在(k,k+1)(k
在(k,k+1)(k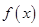 满足条件;①对任意的
满足条件;①对任意的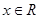 ,都有
,都有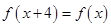 ;②对任意的
;②对任意的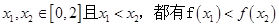 ;③函数
;③函数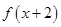 的图象关于y轴对称.则下列结论正确的是( )
的图象关于y轴对称.则下列结论正确的是( )
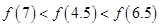
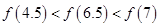
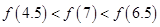
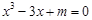 在
在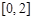 上有解,则实数
上有解,则实数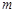 的取值范围是( )
的取值范围是( )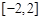
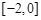
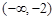 ∪
∪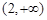
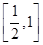 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.