题目内容
已知函数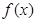 对任意实数
对任意实数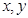 恒有
恒有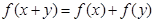 且当
且当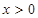 时,有
时,有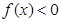 且
且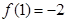 .
.
(1)判断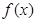 的奇偶性;
的奇偶性;
(2)求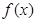 在区间
在区间 上的最大值;
上的最大值;
(3)解关于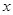 的不等式
的不等式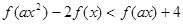 .
.
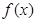 对任意实数
对任意实数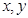 恒有
恒有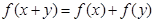 且当
且当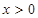 时,有
时,有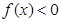 且
且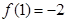 .
.(1)判断
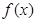 的奇偶性;
的奇偶性;(2)求
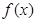 在区间
在区间 上的最大值;
上的最大值;(3)解关于
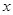 的不等式
的不等式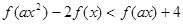 .
.(1)奇函数;(2)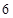 ;
;
(3)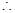 当
当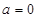 时,
时,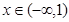
当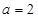 时,
时,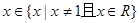
当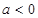 时,
时,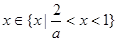
当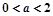 时,
时, 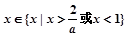
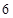 ;
;(3)
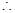 当
当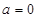 时,
时,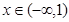
当
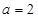 时,
时,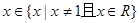
当
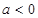 时,
时,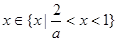
当
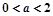 时,
时, 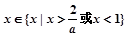
试题分析:(1)赋值法:先令
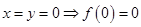 ,再令
,再令
(2)根据
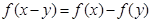 以及当
以及当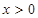 时,有
时,有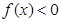 ,利用函数单调性的定义判断得出
,利用函数单调性的定义判断得出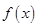 为
为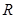 上的减函数;并由单调性求其最值;
上的减函数;并由单调性求其最值;(3)由(1)和(2)的结论,先将不等式
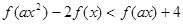 化为
化为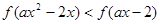 ;再由函数的单调性转化为 关于
;再由函数的单调性转化为 关于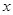 的不等式
的不等式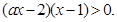 对
对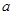 的不同取值,分别讨论不等式的解.
的不同取值,分别讨论不等式的解.试题解析:解(1)取
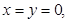 则
则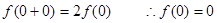
取
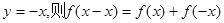
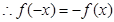 对任意
对任意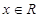 恒成立 ∴
恒成立 ∴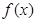 为奇函数.
为奇函数.(2)任取
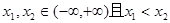 , 则
, 则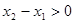
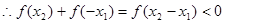
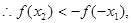 又
又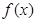 为奇函数
为奇函数 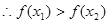
∴
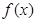 在(-∞,+∞)上是减函数.
在(-∞,+∞)上是减函数.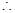 对任意
对任意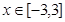 ,恒有
,恒有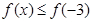
而

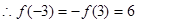 ∴
∴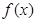 在[-3,3]上的最大值为6
在[-3,3]上的最大值为6(3)∵
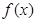 为奇函数,∴整理原式得
为奇函数,∴整理原式得 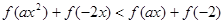
进一步可得
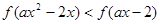
而
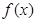 在(-∞,+∞)上是减函数,
在(-∞,+∞)上是减函数,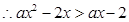
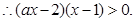
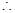 当
当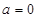 时,
时,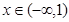
当
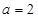 时,
时,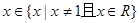
当
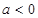 时,
时,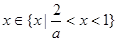
当
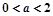 时,
时, 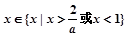

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
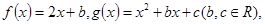 对任意的
对任意的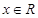 恒有
恒有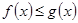 成立.
成立.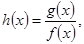 如果
如果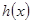 为奇函数,求b,c满足的条件;
为奇函数,求b,c满足的条件;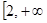 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;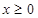 时,
时,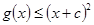 成立;
成立;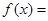
 则满足
则满足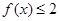 的
的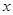 的取值范围是 .
的取值范围是 .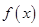 满足条件;①对任意的
满足条件;①对任意的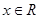 ,都有
,都有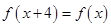 ;②对任意的
;②对任意的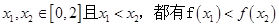 ;③函数
;③函数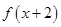 的图象关于y轴对称.则下列结论正确的是( )
的图象关于y轴对称.则下列结论正确的是( )
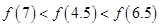
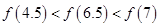
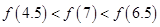
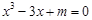 在
在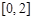 上有解,则实数
上有解,则实数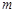 的取值范围是( )
的取值范围是( )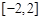
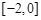
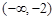 ∪
∪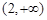
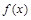 的定义域为A,若
的定义域为A,若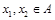 且
且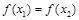 时总有
时总有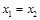 ,则称
,则称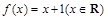 是单函数.下列命题:
是单函数.下列命题: 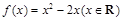 是单函数;
是单函数;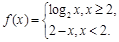 是单函数;
是单函数;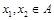 且
且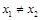 ,则
,则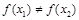 ;
;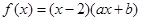 为偶函数,且在
为偶函数,且在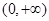 单调递增,则
单调递增,则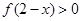 的解集为( )
的解集为( )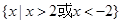

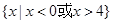

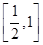 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.