题目内容
已知函数f(x)=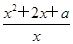 ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=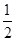 时,求f(x)的最小值;
时,求f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
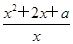 ,x∈[1,+∞).
,x∈[1,+∞).(1)当a=
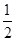 时,求f(x)的最小值;
时,求f(x)的最小值;(2)若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
(1)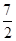 (2)a>-3
(2)a>-3
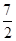 (2)a>-3
(2)a>-3(1)当a=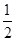 时,f(x)=x+
时,f(x)=x+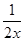 +2.
+2.
设x1>x2≥1,则f(x1)-f(x2)=(x1-x2)+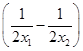 =(x1-x2)·
=(x1-x2)·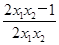 .
.
∵x1>x2≥1,∴f(x1)>f(x2),∴f(x)在[1,+∞)上为增函数.
∴f(x)≥f(1)=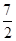 ,即f(x)的最小值为
,即f(x)的最小值为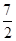 .
.
(2)∵f(x)>0在x∈[1,+∞)上恒成立,
即x2+2x+a>0在[1,+∞)上恒成立,
∴a>[-(x2+2x)]max.
∵t(x)=-(x2+2x)在[1,+∞)上为减函数,
∴t(x)max=t(1)=-3,∴a>-3.
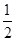 时,f(x)=x+
时,f(x)=x+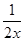 +2.
+2.设x1>x2≥1,则f(x1)-f(x2)=(x1-x2)+
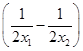 =(x1-x2)·
=(x1-x2)·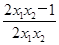 .
.∵x1>x2≥1,∴f(x1)>f(x2),∴f(x)在[1,+∞)上为增函数.
∴f(x)≥f(1)=
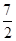 ,即f(x)的最小值为
,即f(x)的最小值为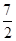 .
.(2)∵f(x)>0在x∈[1,+∞)上恒成立,
即x2+2x+a>0在[1,+∞)上恒成立,
∴a>[-(x2+2x)]max.
∵t(x)=-(x2+2x)在[1,+∞)上为减函数,
∴t(x)max=t(1)=-3,∴a>-3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
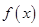 满足条件;①对任意的
满足条件;①对任意的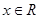 ,都有
,都有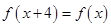 ;②对任意的
;②对任意的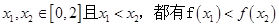 ;③函数
;③函数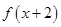 的图象关于y轴对称.则下列结论正确的是( )
的图象关于y轴对称.则下列结论正确的是( )
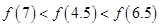
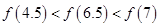
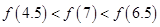
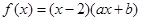 为偶函数,且在
为偶函数,且在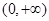 单调递增,则
单调递增,则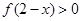 的解集为( )
的解集为( )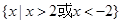

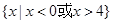

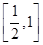 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.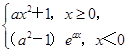 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.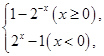 则该函数是( )
则该函数是( )