题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 为其中心.面
为其中心.面![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.

(1)证明:![]() 面
面![]() ;
;
(2)求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:
(1)连结![]() ,由重心的性质可得在
,由重心的性质可得在![]() 中有
中有![]() ,则
,则![]() ,结合线面平行的判定定理可得
,结合线面平行的判定定理可得![]() 平面
平面![]() .
.
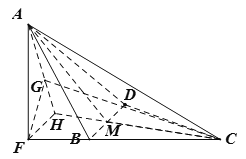
(2)解法一:作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,由题意可得
,由题意可得![]() 为
为![]() 与面
与面![]() 所成角,
所成角,![]() .
.
解法二:以![]() 中点为原点,建立空间直角坐标系.可得
中点为原点,建立空间直角坐标系.可得![]() ,面
,面![]() 的法向量为
的法向量为![]() ,则所求角的正弦值
,则所求角的正弦值![]() .
.
试题解析:
(1)连结![]() ,因为
,因为![]() 是正三角形
是正三角形![]() 的中心,所以
的中心,所以![]() 在
在![]() 上且
上且![]() ,又
,又![]() ,所以在
,所以在![]() 中有
中有![]() ,
,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解法一:作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]()
![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
由面![]() 面
面![]() 知
知![]() 面
面![]() ,所以
,所以![]() ,又
,又![]()
![]() ,所以
,所以![]()
![]()
所以![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() ,作
,作![]() ,则
,则![]() 面
面![]()
连结![]() ,则
,则![]() 为
为![]() 与面
与面![]() 所成角,
所成角,
∴![]() ,即所求角的正弦值为
,即所求角的正弦值为![]() .
.
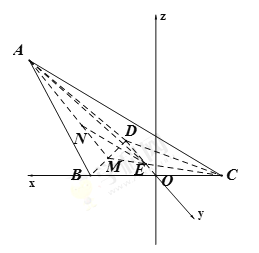
解法二:以![]() 中点为原点,建立如图所示的空间直角坐标系.
中点为原点,建立如图所示的空间直角坐标系.
∵![]() ,
, ![]()
∴![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]() ,则
,则
取![]() ,
,
∴![]() ,即所求角的正弦值为
,即所求角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数X的分布列为
X | 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.Y表示经销一件该商品的利润.
(1)求事件:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(2)求Y的分布列及E(Y).