题目内容
【题目】将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图， 弧AC 长为 
，弧A1B1 长为 
，其中B1与C在平面AA1O1O的同侧．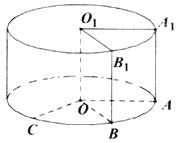 
（1）求圆柱的体积与侧面积；
（2）求异面直线O1B1与OC所成的角的大小．
【答案】
（1）
解：）由题意可知，圆柱的母线长 
，底面半径 
．
圆柱的体积 
，
圆柱的侧面积 
（2）
设过点 
的母线与下底面交于点 
，则 
，
所以 
或其补角为 
与 
所成的角．
由 弧A1B1 长为 
，可知 
，由 弧AC 长为 
，可知 
， 
，
所以异面直线 与 所成的角的大小为 
．
【解析】本题考查几何体的体积侧面积的求法，考查两直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
（1）由题意可知，圆柱的高 
，底面半径 ．计算体积与侧面积即得．
（2）由 得 或其补角为 与 所成的角，计算 即得．
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．
练习册系列答案
名校课堂系列答案
相关题目
