题目内容
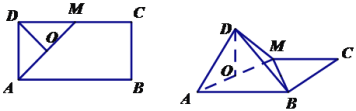
【题目】如图,在矩形ABCD中,AB=2BC=2,点M为DC的中点,将△ADM沿AM折起,使得平面△ADM⊥平面ABCM.

(1)求证:AD⊥BM;
(2)求点C到平面BDM的距离.
【答案】(1)见解析(2)![]()
【解析】
(1)取AM中点O,连结DO,可得DO⊥BM,AM⊥BM,MB⊥平面ADM,即可得BM⊥AD;
(2)![]() ,记点C到平面BDM的距离为h,VC﹣BDM═
,记点C到平面BDM的距离为h,VC﹣BDM═![]() ,又VD-BCM=VC-BDM,即可得点C到平面BDM的距离.
,又VD-BCM=VC-BDM,即可得点C到平面BDM的距离.
(1)取AM中点O,连结DO,
因为平面ADM⊥平面ABCM,AD=DM,
所以OD⊥平面ABCM,DO⊥BM,
易知AM⊥BM,
所以MB⊥平面ADM,
所以BM⊥AD;
(2)∵在矩形ADCB中,AB=2BC=2,点M为DC的中点,
∴DM=CM=![]() ,BM=AM=
,BM=AM=![]() =
=![]() ,DO=
,DO=![]() ,
,
由(1)知MB⊥平面ADM,DM平面ADM,
∴BM⊥DM,S△BDM=![]() .,
.,
又∵DO⊥平面ABCM,
∴![]() ×
×![]() =
=![]() .,
.,
记点C到平面BDM的距离为h,
∴VC-BDM═![]() ,
,
又∵VD-BCM=VC-BDM
∴![]() ,解得h=
,解得h=![]() ,
,
∴点C到平面BDM的距离为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】《山东省高考改革试点方案》规定:从![]() 年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为
年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为![]() 八个等级.参照正态分布原则,确定各等级人数所占比例分别为
八个等级.参照正态分布原则,确定各等级人数所占比例分别为![]() .选考科目成绩计入考生总成绩时,将
.选考科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到
等级内的考生原始成绩,依照等比例转换法则,分别转换到![]()
![]() 八个分数区间,得到考生的等级成绩.
八个分数区间,得到考生的等级成绩.

某校![]() 级学生共
级学生共![]() 人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级
人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级![]() 的学生原始成绩统计如下
的学生原始成绩统计如下
成绩 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人数 | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)求物理获得等级![]() 的学生等级成绩的平均分(四舍五入取整数);
的学生等级成绩的平均分(四舍五入取整数);
(2)从物理原始成绩不小于![]() 分的学生中任取
分的学生中任取![]() 名同学,求
名同学,求![]() 名同学等级成绩不相等的概率.
名同学等级成绩不相等的概率.



