题目内容
【题目】在三棱柱![]() 中,底面
中,底面![]() 是正三角形,侧棱
是正三角形,侧棱![]() 底面
底面![]() .D,E分别是边BC,AC的中点,线段
.D,E分别是边BC,AC的中点,线段![]() 与
与![]() 交于点G,且
交于点G,且![]() ,
,![]() .
.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求证:![]() ⊥平面
⊥平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)证明EG∥AB1.然后利用直线与平面平行的判定定理证明EG∥平面AB1D.
(2)取B1C1的中点D1,连接DD1.建立空间直角坐标系D-xyz,通过向量的数量积证明BC1⊥DA,BC1⊥DB1.然后证明BC1⊥平面AB1D.
(3)求出平面B1CB的一个法向量,平面AB1C的一个法向量,设二面角A-B1C-B的平面角为θ,利用空间向量的数量积求解二面角的余弦函数值即可.
(1)证明:因为E为AC中点,G为B1C中点.所以EG∥AB1.
又因为EG平面AB1D,AB1平面AB1D,
所以EG∥平面AB1D.
(2)证明:取B1C1的中点D1,连接DD1.
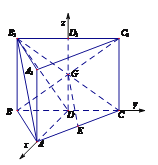
显然DA,DC,DD1两两互相垂直,如图,建立空间直角坐标系D-xyz,
则D(0,0,0),![]() ,B(0,-2,0),
,B(0,-2,0),![]() ,
,![]() ,
,![]() ,C(0,2,0).
,C(0,2,0).
所以![]() ,
,![]() ,
,![]() .
.
又因为![]() ,
,![]() ,
,
所以BC1⊥DA,BC1⊥DB1.
又因为DA∩DB1=D,所以BC1⊥平面AB1D.
(3)解:显然平面B1CB的一个法向量为![]() =(1,0,0).
=(1,0,0).
设平面AB1C的一个法向量为:![]() =(x,y,z),
=(x,y,z),
又![]() ,
,![]() ,
,
由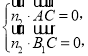 得
得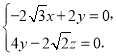
设x=1,则![]() ,
,![]() ,则
,则![]() .
.
所以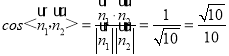 .
.
设二面角A-B1C-B的平面角为θ,由图可知此二面角为锐二面角,
所以![]() .
.

【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,![]() 年
年![]() 月
月![]() 日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为
日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为![]() 元;(2)每月应纳税所得额(含税)
元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等,其中前两项的扣除标准为:①赡养老人费用:每月扣除
等,其中前两项的扣除标准为:①赡养老人费用:每月扣除![]() 元②子女教育费用:每个子女每月扣除
元②子女教育费用:每个子女每月扣除![]() 元
元
新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过 | 超过 | 超过 | 超过 |
|
税率 |
|
|
|
|
|
(1)现有李某月收入![]() 元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?
元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?
(2)现收集了某城市![]() 名年龄在
名年龄在![]() 岁到
岁到![]() 岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有
岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有![]() 人,没有孩子的有
人,没有孩子的有![]() 人,有一个孩子的人中有
人,有一个孩子的人中有![]() 人需要赡养老人,没有孩子的人中有
人需要赡养老人,没有孩子的人中有![]() 人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的
人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的![]() 人中,任何两人均不在一个家庭).若他们的月收入均为
人中,任何两人均不在一个家庭).若他们的月收入均为![]() 元,试求在新个税政策下这
元,试求在新个税政策下这![]() 名公司白领的月平均缴纳个税金额为多少?
名公司白领的月平均缴纳个税金额为多少?
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() .
.
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?