题目内容
已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).
(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
(1)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(2)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M,N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析学生错解:解:(1)曲线C是焦点在x轴上的椭圆,当且仅当 解得2<m<5,所以m的取值范围是(2,5).
解得2<m<5,所以m的取值范围是(2,5).
(2)当m=4时,曲线C的方程为x2+2y2=8,点A,B的坐标分别为(0,2),(0,-2).
由 得(1+2k2)x2+16kx+24=0.
得(1+2k2)x2+16kx+24=0.
设点M,N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,x1+x2= ,x1x2=
,x1x2= .直线BM的方程为y+2=
.直线BM的方程为y+2= x,点G的坐标为
x,点G的坐标为 .
.
因为直线AN和直线AG的斜率分别为kAN= ,kAG=-
,kAG=- ,所以kAN-kAG=
,所以kAN-kAG=
 =
= =
= =
= =0.
=0.
即kAN=kAG.故A,G,N三点共线.
审题引导:(1)方程的曲线是焦点在x轴上的椭圆;
(2)证明三点共线的常用方法.
规范解答:解:(1)曲线C是焦点在x轴上的椭圆,当且仅当 (3分)
(3分)
解得 <m<5,所以m的取值范围是
<m<5,所以m的取值范围是 .(4分)
.(4分)
(2)当m=4时,曲线C的方程为x2+2y2=8,点A,B的坐标分别为(0,2),(0,-2).(5分)
由 得(1+2k2)x2+16kx+24=0.(6分)
得(1+2k2)x2+16kx+24=0.(6分)
因为直线与曲线C交于不同的两点,所以Δ=(16k)2-4(1+2k2)×24>0,即k2> .(7分)
.(7分)
设点M,N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,
x1+x2= ,x1x2=
,x1x2= .(8分)
.(8分)
直线BM的方程为y+2= x,点G的坐标为
x,点G的坐标为 .(9分)
.(9分)
因为直线AN和直线AG的斜率分别为kAN= ,kAG=-
,kAG=- ,(11分)
,(11分)
所以kAN-kAG= =0.
=0.
即kAN=kAG.(13分)故A,G,N三点共线.(14分)
错因分析:易忽视焦点在x轴上,漏掉 这一条件,从而失误.联立消元后易忽视Δ>0这一前提条件.
这一条件,从而失误.联立消元后易忽视Δ>0这一前提条件.
 解得2<m<5,所以m的取值范围是(2,5).
解得2<m<5,所以m的取值范围是(2,5).(2)当m=4时,曲线C的方程为x2+2y2=8,点A,B的坐标分别为(0,2),(0,-2).
由
 得(1+2k2)x2+16kx+24=0.
得(1+2k2)x2+16kx+24=0.设点M,N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,x1+x2=
 ,x1x2=
,x1x2= .直线BM的方程为y+2=
.直线BM的方程为y+2= x,点G的坐标为
x,点G的坐标为 .
.因为直线AN和直线AG的斜率分别为kAN=
 ,kAG=-
,kAG=- ,所以kAN-kAG=
,所以kAN-kAG= =
= =
= =
= =0.
=0.即kAN=kAG.故A,G,N三点共线.
审题引导:(1)方程的曲线是焦点在x轴上的椭圆;
(2)证明三点共线的常用方法.
规范解答:解:(1)曲线C是焦点在x轴上的椭圆,当且仅当
 (3分)
(3分)解得
 <m<5,所以m的取值范围是
<m<5,所以m的取值范围是 .(4分)
.(4分) (2)当m=4时,曲线C的方程为x2+2y2=8,点A,B的坐标分别为(0,2),(0,-2).(5分)
由
 得(1+2k2)x2+16kx+24=0.(6分)
得(1+2k2)x2+16kx+24=0.(6分) 因为直线与曲线C交于不同的两点,所以Δ=(16k)2-4(1+2k2)×24>0,即k2>
 .(7分)
.(7分)设点M,N的坐标分别为(x1,y1),(x2,y2),则y1=kx1+4,y2=kx2+4,
x1+x2=
 ,x1x2=
,x1x2= .(8分)
.(8分)直线BM的方程为y+2=
 x,点G的坐标为
x,点G的坐标为 .(9分)
.(9分)因为直线AN和直线AG的斜率分别为kAN=
 ,kAG=-
,kAG=- ,(11分)
,(11分)所以kAN-kAG=
 =0.
=0.即kAN=kAG.(13分)故A,G,N三点共线.(14分)
错因分析:易忽视焦点在x轴上,漏掉
 这一条件,从而失误.联立消元后易忽视Δ>0这一前提条件.
这一条件,从而失误.联立消元后易忽视Δ>0这一前提条件.
练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 、
、 , 焦距为2,过
, 焦距为2,过 为3
为3  交椭圆于A、B两点,判断是否存在直线
交椭圆于A、B两点,判断是否存在直线 为钝角,若存在,求出直线
为钝角,若存在,求出直线 的取值范围
的取值范围 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
 的中心在原点、焦点在
的中心在原点、焦点在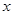 轴上,抛物线
轴上,抛物线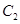 的顶点在原点、焦点在
的顶点在原点、焦点在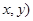 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆











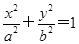 =1(a>b>0),点P
=1(a>b>0),点P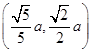 在椭圆上.
在椭圆上. +y2=1的左右焦点,点P在椭圆上运动.则
+y2=1的左右焦点,点P在椭圆上运动.则 的最大值是________.
的最大值是________.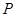 是椭圆
是椭圆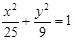 上的点,
上的点, 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若 ,则
,则 的面积为( )
的面积为( )


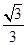
 -
-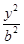 =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆 +
+ =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .