题目内容
已知双曲线 -
-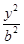 =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆 +
+ =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
 -
-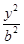 =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆 +
+ =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .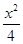 -
-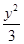 =1
=1椭圆 +
+ =1的焦点坐标为F1(-
=1的焦点坐标为F1(-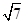 ,0),F2(
,0),F2(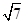 ,0),离心率为e=
,0),离心率为e=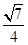 .
.
由于双曲线 -
-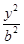 =1与椭圆
=1与椭圆 +
+ =1有相同的焦点,
=1有相同的焦点,
因此a2+b2=7.
又双曲线的离心率e=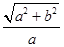 =
=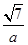 ,
,
所以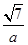 =
=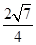 ,
,
所以a=2,b2=c2-a2=3,
故双曲线的方程为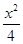 -
-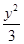 =1.
=1.
 +
+ =1的焦点坐标为F1(-
=1的焦点坐标为F1(-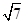 ,0),F2(
,0),F2(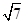 ,0),离心率为e=
,0),离心率为e=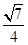 .
.由于双曲线
 -
-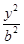 =1与椭圆
=1与椭圆 +
+ =1有相同的焦点,
=1有相同的焦点,因此a2+b2=7.
又双曲线的离心率e=
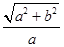 =
=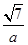 ,
,所以
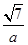 =
=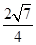 ,
,所以a=2,b2=c2-a2=3,
故双曲线的方程为
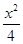 -
-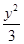 =1.
=1.
练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 、
、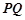 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 ,直线
,直线 .
.
 ,
, ,求
,求 的值;
的值; 变化时,恒有
变化时,恒有 的焦距为2,则m的取值是 ( )
的焦距为2,则m的取值是 ( ) ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点, =4.
=4.
 +
+ =1(a>0,b>0)的右焦点为F(3,0),且点(-3,
=1(a>0,b>0)的右焦点为F(3,0),且点(-3,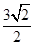 )在椭圆C上,则椭圆C的标准方程为 .
)在椭圆C上,则椭圆C的标准方程为 . +
+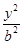 =1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4
=1的长半轴长和短半轴长,若此椭圆的一焦点与抛物线y2=4 x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( ) +
+ =1
=1 +
+ =1
=1 =1
=1 +
+ =1
=1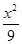 +
+ =1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .
=1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 . +
+ =1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴,
=1(a>b>0)的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM∥x轴, ·
· =9,若点P的坐标为(0,t),则t的取值范围是( )
=9,若点P的坐标为(0,t),则t的取值范围是( )
