题目内容
已知椭圆 的中心在原点、焦点在
的中心在原点、焦点在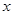 轴上,抛物线
轴上,抛物线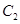 的顶点在原点、焦点在
的顶点在原点、焦点在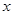 轴上.小明从曲线
轴上.小明从曲线 、
、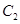 上各取若干个点(每条曲线上至少取两个点),并记录其坐标(
上各取若干个点(每条曲线上至少取两个点),并记录其坐标(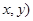 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆 上,也不在抛物线
上,也不在抛物线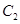 上,小明的记录如下:
上,小明的记录如下:
据此,可推断椭圆 的方程为
的方程为
 的中心在原点、焦点在
的中心在原点、焦点在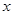 轴上,抛物线
轴上,抛物线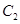 的顶点在原点、焦点在
的顶点在原点、焦点在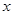 轴上.小明从曲线
轴上.小明从曲线 、
、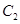 上各取若干个点(每条曲线上至少取两个点),并记录其坐标(
上各取若干个点(每条曲线上至少取两个点),并记录其坐标(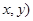 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆 上,也不在抛物线
上,也不在抛物线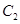 上,小明的记录如下:
上,小明的记录如下: |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 的方程为
的方程为 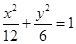
试题分析:由题意可知:点(0,
 )是椭圆
)是椭圆 的短轴的一个端点,或点(?
的短轴的一个端点,或点(? ,0)是椭圆
,0)是椭圆 的长轴的一个端点.以下分两种情况讨论:
的长轴的一个端点.以下分两种情况讨论:假设点(0,
 )是椭圆
)是椭圆 的短轴的一个端点,则
的短轴的一个端点,则 可以写成
可以写成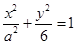 ,经验证可得:若点(
,经验证可得:若点( ,
, )在
)在 上,代入求得
上,代入求得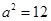 ,即
,即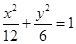 ,剩下的4个点中(-2,2)也在此椭圆上.
,剩下的4个点中(-2,2)也在此椭圆上.假设抛物线
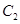 的方程为
的方程为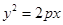 ,把点(2,
,把点(2, )代入求得p=2,∴
)代入求得p=2,∴ ,则点(3,
,则点(3, ),则只剩下一个点(
),则只剩下一个点( ,0)既不在椭圆上,也不在抛物线上,满足条件.
,0)既不在椭圆上,也不在抛物线上,满足条件.假设抛物线
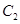 的方程为
的方程为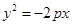 ,经验证不符合题意.
,经验证不符合题意.假设点(?
 ,0)是椭圆
,0)是椭圆 的长轴的一个端点,则
的长轴的一个端点,则 可以写成
可以写成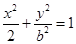 ,经验证不满足条件,应舍去.综上可知:可推断椭圆
,经验证不满足条件,应舍去.综上可知:可推断椭圆 的方程为
的方程为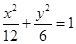 ,故答案为
,故答案为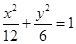 .
.
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点. 的取值范围;
的取值范围; 轴的对称点是
轴的对称点是 ,证明:直线
,证明:直线 恒过一定点.
恒过一定点. 的右焦点重合,直线
的右焦点重合,直线 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点. ,m、n是实数,对于直线
,m、n是实数,对于直线 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 的直线
的直线 与椭圆
与椭圆 (点
(点 为椭圆
为椭圆 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由. 的离心率为( )
的离心率为( )

 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为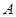 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.
 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.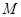 是椭圆
是椭圆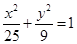 上的点,
上的点,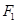 、
、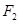 是椭圆的两个焦点,
是椭圆的两个焦点,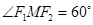 ,则
,则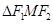 的面积等于______________.
的面积等于______________.