题目内容
如图,在平面直角坐标系xOy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.

(1)求点B的轨迹方程;
(2)当点D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆C上的另一个动点,且满足FG⊥FE,记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由.

(1)求点B的轨迹方程;
(2)当点D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆C上的另一个动点,且满足FG⊥FE,记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由.
(1)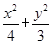 =1(2)x-2y+4=0(3)
=1(2)x-2y+4=0(3)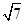
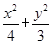 =1(2)x-2y+4=0(3)
=1(2)x-2y+4=0(3)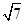
(1)连结BF,由已知BF=BE,所以BC+BF=BC+BE=CE=4,
所以点B的轨迹是以C、F为焦点,长轴为4的椭圆,所以B点的轨迹方程为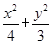 =1.
=1.
(2)当点D位于y轴的正半轴上时,因为D是线段EF的中点,O为线段CF的中点,所以CE∥OD,且CE=2OD,所以E、D的坐标分别为(-1,4)和(0,2).
因为PQ是线段EF的垂直平分线,所以直线PQ的方程为y=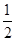 x+2,即直线PQ的方程为x-2y+4=0.
x+2,即直线PQ的方程为x-2y+4=0.
(3)设点E、G的坐标分别为(x1,y1)和(x2,y2),则点M的坐标为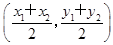 ,因为点E、G均在圆C上,且FG⊥FE,所以(x1+1)2+
,因为点E、G均在圆C上,且FG⊥FE,所以(x1+1)2+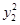 =16,①,(x2+1)2+
=16,①,(x2+1)2+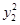 =16,②
=16,②
(x1-1)(x2-1)+y1y2=0,③
所以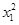 +
+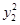 =15-2x1,
=15-2x1,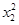 +
+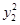 =15-2x2,x1x2+y1y2=x1+x2-1.所以MO2=
=15-2x2,x1x2+y1y2=x1+x2-1.所以MO2=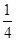 [(x1+x2)2+(y1+y2)2]=
[(x1+x2)2+(y1+y2)2]=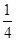 ·[(
·[(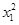 +
+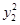 )+(
)+(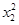 +
+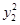 )+2(x1x2+y1y2)]=
)+2(x1x2+y1y2)]=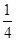 [15-2x1+15-2x2+2(x1+x2-1)]=7,即M点到坐标原点O的距离为定值,且定值为
[15-2x1+15-2x2+2(x1+x2-1)]=7,即M点到坐标原点O的距离为定值,且定值为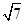 .
.
所以点B的轨迹是以C、F为焦点,长轴为4的椭圆,所以B点的轨迹方程为
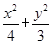 =1.
=1.(2)当点D位于y轴的正半轴上时,因为D是线段EF的中点,O为线段CF的中点,所以CE∥OD,且CE=2OD,所以E、D的坐标分别为(-1,4)和(0,2).
因为PQ是线段EF的垂直平分线,所以直线PQ的方程为y=
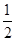 x+2,即直线PQ的方程为x-2y+4=0.
x+2,即直线PQ的方程为x-2y+4=0.(3)设点E、G的坐标分别为(x1,y1)和(x2,y2),则点M的坐标为
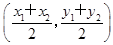 ,因为点E、G均在圆C上,且FG⊥FE,所以(x1+1)2+
,因为点E、G均在圆C上,且FG⊥FE,所以(x1+1)2+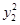 =16,①,(x2+1)2+
=16,①,(x2+1)2+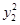 =16,②
=16,②(x1-1)(x2-1)+y1y2=0,③
所以
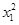 +
+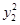 =15-2x1,
=15-2x1,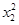 +
+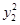 =15-2x2,x1x2+y1y2=x1+x2-1.所以MO2=
=15-2x2,x1x2+y1y2=x1+x2-1.所以MO2=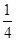 [(x1+x2)2+(y1+y2)2]=
[(x1+x2)2+(y1+y2)2]=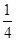 ·[(
·[(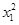 +
+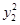 )+(
)+(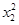 +
+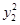 )+2(x1x2+y1y2)]=
)+2(x1x2+y1y2)]=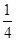 [15-2x1+15-2x2+2(x1+x2-1)]=7,即M点到坐标原点O的距离为定值,且定值为
[15-2x1+15-2x2+2(x1+x2-1)]=7,即M点到坐标原点O的距离为定值,且定值为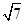 .
.
练习册系列答案
相关题目
 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点. 的取值范围;
的取值范围; 轴的对称点是
轴的对称点是 ,证明:直线
,证明:直线 恒过一定点.
恒过一定点. :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 的直线
的直线 与椭圆
与椭圆 (点
(点 为椭圆
为椭圆 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
 )的直线与椭圆交于A、B两点,与直线y=2交于点M(直线AB不经过P点),记PA、PB、PM的斜率分别为k1、k2、k3,问:是否存在常数
)的直线与椭圆交于A、B两点,与直线y=2交于点M(直线AB不经过P点),记PA、PB、PM的斜率分别为k1、k2、k3,问:是否存在常数 ,使得
,使得 若存在,求出名
若存在,求出名 、
、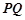 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 ,直线
,直线 .
.
 ,
, ,求
,求 的值;
的值; 变化时,恒有
变化时,恒有 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
 的直线l与椭圆
的直线l与椭圆 =1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.
=1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.