题目内容
12.现有3位老师去参加学校组织的春季娱乐活动,该活动有甲、乙两个游戏可供选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏,且每个人参加游戏互不影响,设X表示参加甲游戏的人数,求随机变量X的分布列.分析 根据题意,求出某位教师参加甲游戏的概率P,得出X的可能取值,计算对应的概率,列出分布列即可.
解答 解:由题意知,某位教师去参加甲游戏的概率为P=$\frac{2}{6}$=$\frac{1}{3}$,
且X的可能取值分别为0,1,2,3;
所以,P(X=0)=${C}_{3}^{0}$•${(\frac{1}{3})}^{0}$•${(1-\frac{1}{3})}^{3}$=$\frac{8}{27}$,
P(X=1)=${C}_{3}^{1}$•${(\frac{1}{3})}^{1}$•${(1-\frac{1}{3})}^{2}$=$\frac{12}{27}$,
P(X=2)=${C}_{3}^{2}$•${(\frac{1}{3})}^{2}$${(1-\frac{1}{3})}^{1}$=$\frac{6}{27}$
P(X=3)=${C}_{3}^{3}$•${(\frac{1}{3})}^{3}$•${(1-\frac{1}{3})}^{0}$=$\frac{1}{27}$;
所以X的分布列如下;
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{12}{27}$ | $\frac{6}{27}$ | $\frac{1}{27}$ |
点评 本题考查了离散型随机变量的分布列的应用问题,是基础题目.

练习册系列答案
相关题目
2.当x∈[-4,0]时,a+$\sqrt{-{x^2}-4x}$≤$\frac{4}{3}$x+1恒成立,则a的一个可能的值是( )
| A. | 5 | B. | $\frac{5}{3}$ | C. | $-\frac{5}{3}$ | D. | -5 |
3.一个工厂为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
(1)画出散点图;
(2)推出是正相关还是负相关;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| 零件数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)推出是正相关还是负相关;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
4.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥a}\\{x-y≤-1}\end{array}\right.$,且z=x+ay,则( )
| A. | 当a>0时有最大值 | B. | 当a>1时有最小值 | ||
| C. | 当a<0时有最大值 | D. | 当0<a<1时有最小值 |
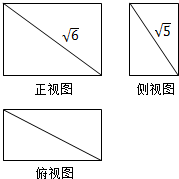 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.