Question

3．一个工厂为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，收集数据如下：

零件数	10	20	30	40	50	60	70	80	90	100
加工时间	62	68	75	81	89	95	102	108	115	122

（1）画出散点图；
（2）推出是正相关还是负相关；
（3）关于加工零件的个数与加工时间，你能得出什么结论？

Answer 1

分析 （1）根据所给数据，可得散点图；
（2）利用公式求出b，即可得出结论；
（3）这个回归直线方程的意义是当x每增大1时，y的值约增加0.668．

解答 解：（1）散点图如图所示：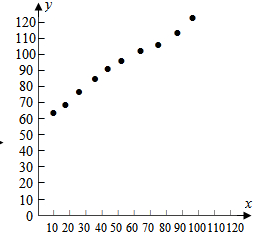

（2）$\overline{x}$=55，$\overline{y}$=91.7，$\sum_{i=1}^{10}{{x}_{i}}^{2}$=38500，$\sum_{i=1}^{10}$${{y}_{i}}^{2}$=87777，$\sum_{i=1}^{10}$x_iy_i=55950，
因此b=$\frac{55950-10×55×91.7}{38500-10×5{5}^{2}}$≈0.668＞0，
因此是正相关；
（3）这个回归直线方程的意义是当x每增大1时，y的值约增加0.668．

点评 本题考查散点图，考查线性回归方程，考查学生的计算能力，比较基础．