题目内容
20.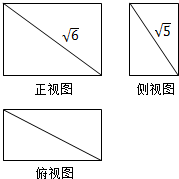 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
分析 设长方体的长,宽,高分别为x,y,z,根据已知求出长宽高,代入长方体表面积公式,可得答案.
解答 解:设长方体的长,宽,高分别为x,y,z,
由题意得:$\left\{\begin{array}{l}{x}^{2}+{y}^{2}=5\\{x}^{2}+{z}^{2}=10\\{y}^{2}+{z}^{2}=6\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=\frac{3\sqrt{2}}{2}\\ y=\frac{\sqrt{2}}{2}\\ z=\frac{\sqrt{22}}{2}\end{array}\right.$,
故该长方体的表面积S=2(xy+xz+yz)=3+4$\sqrt{11}$,
故答案为:3+4$\sqrt{11}$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目