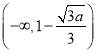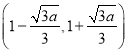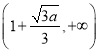Question

【题目】设函数,其中

(Ⅰ)求的单调区间；

（Ⅱ）若存在极值点，且，其中，求证: ；

（Ⅲ）设，函数，求证： 在区间上最大值不小于.

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）见解析;（Ⅲ）见解析.

【解析】试题分析：（1）求单调区间，先求导解导数大于零求递增区间，导数小于零求递减区间，但要注意a的取值对导数符号得影响（2）函数存在极值点，即将代入导函数等于零，又所以从而得证（3）求最值先分析函数单调性即可，然后讨论在区间得极值和端点值大小来确定最大值，再验证其不小于即可

试题解析：

（Ⅰ）由，可得，

下面分两种情况讨论：

（1）当时，有恒成立，所以单调递增区间为

（2）当时，令，解得，或，

当变化时， 的变化情况如下表：

	+	0	-	0	+
	单调递增	极大值	单调递减	极小值	单调递增

所以的单调递减区间为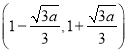，单调递增区间为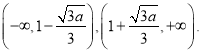

（Ⅱ）证明：因为存在极值点，所以由（Ⅰ）知，且，由题意，得，即

进而

又

,且，由题意及（Ⅰ）知，存在唯一实数满足，且，因此，所以；

（Ⅲ）证明：设在区间上的最大值为, 表示两数的最大值，下面分三种情况讨论：

（1）当时， ，由（Ⅰ）知， 在区间上单调递减，所以在区间上的取值范围为，因此

所以

（2）当时， ，由（Ⅰ）和（Ⅱ）知， ，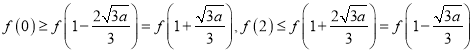

所以在区间上的取值范围为，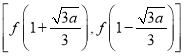

因此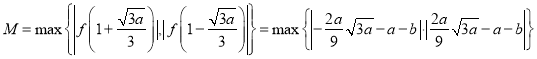

（3）当时 时， ，由（Ⅰ）和（Ⅱ）知， ， ，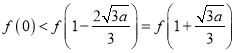

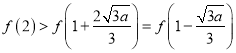所以在区间上的取值范围为，因此，

综上所述，当时， 在区间上的最大值不小于.