题目内容
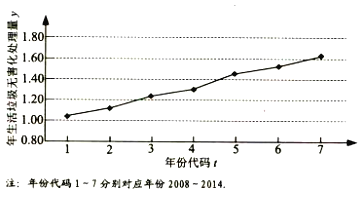
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
(Ⅰ)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
参考数据: ![]() ,
, ![]() ,
, 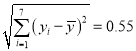 ,
, ![]() .
.
参考公式:相关系数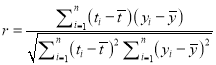 ,
,
回归方程![]() ,
, 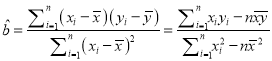 ,
,
本题中斜率和截距的最小二乘估计公式分别为: 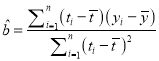 ,
, ![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ) 1.82亿吨.
【解析】试题分析:(1)根据图形可知散点大致分布在一条直线附近,于是先求相关系数,在用线性回归方程模拟即可(2)根据回归方程公式求出回归方程![]() ,将2016年对应的
,将2016年对应的![]() 代入回归方程得
代入回归方程得![]() ,
,
(Ⅰ)由折线图中的数据和附注中的参考数据得
![]() ,
, ![]() ,
,  ,
,
![]() ,
,
∴![]() .
.
因为![]() 与
与![]() 的相关系数近似为0.99,说明
的相关系数近似为0.99,说明![]() 与
与![]() 的线性相关程度相当高,从而可以用线性回归模型拟合
的线性相关程度相当高,从而可以用线性回归模型拟合![]() 与
与![]() 的关系.
的关系.
(Ⅱ)由![]() 及(Ⅰ)得
及(Ⅰ)得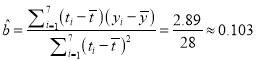 ,
,
![]()
![]() .
.
所以, ![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
将2016年对应的![]() 代入回归方程得
代入回归方程得![]() ,
,
所以预测2016年我国生活垃圾无害化处理量约为1.82亿吨.

【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() 两点,若
两点,若![]() 恰好为线段的三等分点,求直线
恰好为线段的三等分点,求直线![]() 的斜率.
的斜率.
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: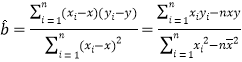 ,
,![]() )
)
【题目】某市2010年至2016年新开楼盘的平均销售价格![]() (单位:千元/平米)的统计数据如下表:
(单位:千元/平米)的统计数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 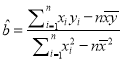 ,
, ![]() .
.