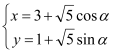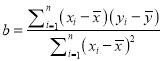题目内容
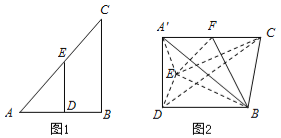
【题目】如图1在![]() △
△![]() 中,
中,![]()
![]() ,
,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .以
.以![]() 为折痕,将
为折痕,将![]() △
△![]() 折起到图2的位置,使平面
折起到图2的位置,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
,![]() ,设
,设![]() 是线段
是线段![]() 上的动点,满足
上的动点,满足![]() .
.
(1)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由已知得![]() ,
,![]() 平面
平面![]() ,从而
,从而![]() ,由
,由![]() ,得
,得![]() ,由此能证明平面
,由此能证明平面![]() ⊥平面
⊥平面![]() ;(2)以
;(2)以![]() 为坐标原点
为坐标原点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,求得平面
轴建立空间直角坐标系,求得平面![]() 的一个法向量为
的一个法向量为![]() ,又知平面
,又知平面![]() 的法向量为
的法向量为![]() ,由此利用空间向量夹角余弦公式余弦公式能求出
,由此利用空间向量夹角余弦公式余弦公式能求出![]() .
.
试题解析:(1)∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() 分别为中点,
分别为中点,
∴![]() ,
,![]() ,
,
在直角三角形![]() 中,
中,![]() .
.
∴![]() ,可得
,可得![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.
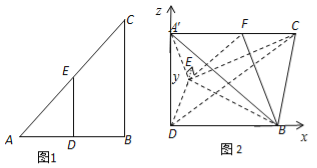
(2)以![]() 为坐标原点
为坐标原点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
各点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
∴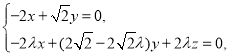 取
取![]() ,
,
又∵平面![]() 的法向量为
的法向量为![]() ,
,
∴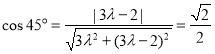 ,化为
,化为![]() ,解得
,解得![]() ,
,
又∵![]() ,∴
,∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】下表提供了某厂生产某产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 2 | 4 | 6 | 8 | 10 |
| 4 | 5 | 7 | 9 | 10 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为: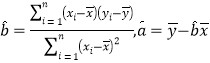 .
.