题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)求证: ![]() ;
;
(3)求证:当![]() 时,
时, ![]() ,
, ![]() 恒成立.
恒成立.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .(2)见解析;(3)见解析.
.(2)见解析;(3)见解析.
【解析】试题分析:(1)求函数![]() 的导数,对
的导数,对![]() 讨论,分当
讨论,分当![]() 时,当
时,当![]() 时,令导数大于0,得增区间,令导数小于0,得减区间;
时,令导数大于0,得增区间,令导数小于0,得减区间;
(2) 令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,不等式得证;
,不等式得证;
(3)构造函数![]() ,证明其最小值大于等于0即可.
,证明其最小值大于等于0即可.
试题解析:(1)![]() ,
,
(ⅰ)当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ⅱ)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减.
单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)证明:令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,即
,即![]() .
.
(3)证明: ![]() 恒成立与
恒成立与![]() 恒成立等价,
恒成立等价,
令![]() ,即
,即![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() (或令
(或令![]() ,则
,则![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() 在
在![]() 上递增,∴
上递增,∴![]() ,∴
,∴![]() )
)
∴![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 恒成立.
恒成立.
点晴:本题主要考查函数单调性,不等式恒成立,及不等式的证明问题.要求单调性,求导比较导方程的根的大小,解不等式可得单调区间,要证明不等式恒成立问题可转化为构造新函数,求其值最值即可.这类问题的通解方法就是:划归与转化之后,就可以假设相对应的函数,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.

【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
【题目】下表提供了某厂生产某产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 2 | 4 | 6 | 8 | 10 |
| 4 | 5 | 7 | 9 | 10 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为: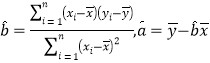 .
.