题目内容

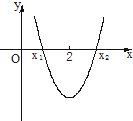
函数f（x）=x2+mx+9在区间（-3，+∞）单调递增，则实数m的取值范围为（　　）
A．（6，+∞）B．[6，+∞）C．（-∞，6）D．（-∞，6]
方法1：导数法
函数的导数为f'（x）=2x+m，要使函数在区间（-3，+∞）单调递增，
即f'（x）=2x+m≥0在[-3，+∞）上恒成立，
所以m≥-2x在[-3，+∞）上恒成立，
所以m≥6．
方法2：函数性质法
二次函数的对称轴为-
m
2
，且函数在[-
m
2
，+∞）上单调递增，
所以要使数在区间（-3，+∞）单调递增，则-
m
2
≤-3．
解得m≥6．
故选B．
练习册系列答案
相关题目
已知函数f（x）=x2+ax+b（a、b∈R），g（x）=2x2-4x-16，
（1）求不等式g（x）＜0的解集；
（2）若|f（x）|≤|g（x）|对任意x∈R恒成立，求a，b；
（3）在（2）的条件下，若对一切x＞2，均有f（x）≥（m+2）x-m-15成立，求实数m的取值范围．
已知f（x）=（x-a）（x-b）+1，并且α，β是方程f（x）=0的两根，则实数α，β，a，b的大小可能是（　　）
A．α＜a＜β＜bB．a＜α＜b＜βC．a＜α＜β＜bD．α＜a＜b＜β
二次函数y=x2+（a-3）x+1的图象与x轴的两个交点的横坐标分别为x1、x2，且x1＜2，x2＞2，如图所示，则a的取值范围是（　　）
A．a＜1或a＞5B．a＜
1
2
C．a＜-
1
2
或a＞5		D．-
1
2
＜a＜1
已知函数f（x）=x2-|4|+3（x∈R），
（I）判断函数的奇偶性并将函数写成分段函数的形式；
（II）画出函数的图象并指出它的单调区间．
已知f（x）=x2-53x+196+|x2-53x+196|，则f（1）+f（2）+…+f（50）=______．
函数y=ax2+bx与y=log|
b
a
|x（ab≠0，|a|≠|b|）在同一直角坐标系中的图象可能是（　　）
A．B．C．D．
已知函数f（x）=（
1
2
）|x|，设a=f（2-0.3），b=f（log20.3），c=f（ln10），则a，b，c的大小关系是（　　）
A．a＞c＞bB．b＞a＞cC．c＞a＞bD．a＞b＞c
已知函数y＝2－x2＋ax＋1在区间(－∞，3)内递增，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网