题目内容
已知函数y＝2－x2＋ax＋1在区间(－∞，3)内递增，求a的取值范围．
[6，＋∞)
解：函数y＝2－x2＋ax＋1是由函数y＝2t和t＝－x2＋ax＋1复合而成．
因为函数t＝－x2＋ax＋1在区间(－∞，
]上单调递增，在区间[，＋∞)上单调递减，且函数y＝2t在R上单调递增，
所以函数y＝2－x2＋ax＋1在区间(－∞，]上单调递增，在区间[，＋∞)上单调递减．
又因为函数y＝2－x2＋ax＋1在区间(－∞，3)内单调递增，所以3≤，
即a≥6.故a的取值范围为[6，＋∞)．
因为函数t＝－x2＋ax＋1在区间(－∞，
]上单调递增，在区间[，＋∞)上单调递减，且函数y＝2t在R上单调递增，所以函数y＝2－x2＋ax＋1在区间(－∞，
]上单调递增，在区间[，＋∞)上单调递减．又因为函数y＝2－x2＋ax＋1在区间(－∞，3)内单调递增，所以3≤
，即a≥6.故a的取值范围为[6，＋∞)．
练习册系列答案
孟建平名校考卷系列答案
相关题目
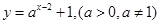的图像过一个定点，则定点的坐标是 
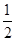)－1.2，则a，b，c的大小关系为( )
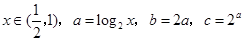，则（ ）
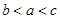
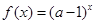在R上是增函数，则
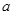的取值范围是（ ）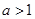 
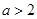
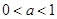
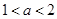
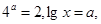则
=________.
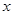，则有（ ）．
