题目内容
已知函数f（x）=x2-|4|+3（x∈R），
（I）判断函数的奇偶性并将函数写成分段函数的形式；
（II）画出函数的图象并指出它的单调区间．
（I）判断函数的奇偶性并将函数写成分段函数的形式；
（II）画出函数的图象并指出它的单调区间．
（I）因为函数的定义域为R，关于坐标原点对称，…（1分）
且f（-x）=（-x）2-4|-x|+3=x2-4|x|+3=f（x），
故函数为偶函数．…（3分）
f（x）=x2-4|x|+3，
…（5分）
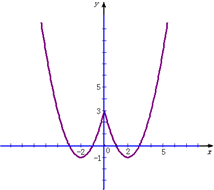
（II）如图…（8分）
单调增区间为（-2，0），[2，+∞），…（9分）
单调减区间为（-∞，-2），[0，2]；…（10分）
且f（-x）=（-x）2-4|-x|+3=x2-4|x|+3=f（x），
故函数为偶函数．…（3分）
f（x）=x2-4|x|+3，
|
（II）如图…（8分）
单调增区间为（-2，0），[2，+∞），…（9分）
单调减区间为（-∞，-2），[0，2]；…（10分）
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
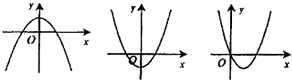
，则有（ ）．
