题目内容
已知函数f(x)=x2+ax+b(a、b∈R),g(x)=2x2-4x-16,
(1)求不等式g(x)<0的解集;
(2)若|f(x)|≤|g(x)|对任意x∈R恒成立,求a,b;
(3)在(2)的条件下,若对一切x>2,均有f(x)≥(m+2)x-m-15成立,求实数m的取值范围.
(1)求不等式g(x)<0的解集;
(2)若|f(x)|≤|g(x)|对任意x∈R恒成立,求a,b;
(3)在(2)的条件下,若对一切x>2,均有f(x)≥(m+2)x-m-15成立,求实数m的取值范围.
(1)g(x)=2x2-4x-16<0,
∴(x+2)(x-4)<0,
∴-2<x<4.
∴不等式g(x)<0的解集为{x|-2<x<4}.…(4分)
(2)∵|x2+ax+b|≤|2x2-4x-16|对x∈R恒成立,
∴当x=4,x=-2时成立,
∴
,
∴
,
∴
.…(8分)
(3)由(2)知,f(x)=x2-2x-8.
∴x2-2x-8≥(m+2)x-m-15 (x>2),
即x2-4x+7≥m(x-1).
∴对一切x>2,均有不等式
≥m成立.…(10分)
而
=(x-1)+
-2
≥2
-2=2(当x=3时等号成立)
∴实数m的取值范围是(-∞,2].…(12分)
∴(x+2)(x-4)<0,
∴-2<x<4.
∴不等式g(x)<0的解集为{x|-2<x<4}.…(4分)
(2)∵|x2+ax+b|≤|2x2-4x-16|对x∈R恒成立,
∴当x=4,x=-2时成立,
∴
|
∴
|
∴
|
(3)由(2)知,f(x)=x2-2x-8.
∴x2-2x-8≥(m+2)x-m-15 (x>2),
即x2-4x+7≥m(x-1).
∴对一切x>2,均有不等式
| x2-4x+7 |
| x-1 |
而
| x2-4x+7 |
| x-1 |
| 4 |
| x-1 |
≥2
(x-1)•
|
∴实数m的取值范围是(-∞,2].…(12分)

练习册系列答案
相关题目
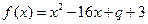 :
: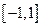 上存在零点,求实数
上存在零点,求实数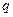 的取值范围;
的取值范围;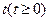 ,当
,当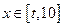 时,
时,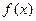 的值域为区间
的值域为区间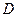 ,且
,且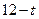 。
。
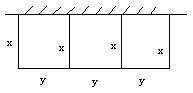
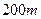 的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?