题目内容
已知f(x)=x2-53x+196+|x2-53x+196|,则f(1)+f(2)+…+f(50)=______.
由x2-53x+196>0得 x>49或x<4,
∴当4≤x≤49时,x2-53x+196≤0,
∴当4≤x≤49时,f(x)=x2-53x+196+|x2-53x+196|=x2-53x+196-(x2-53x+196)=0,
当x>49或x<4时,f(x)=x2-53x+196+|x2-53x+196|=x2-53x+196+(x2-53x+196)=2(x2-53x+196),
∴f(1)+f(2)+…+f(50)=f(1)+f(2)+f(3)+f(50)
∵f(1)=2(1-53+196)=2×144=288,
f(2)=2(4-53×2+196)=2×94=188,
f(3)=2(9-53×3+196)=2×46=92,
f(50)=2(502-53×50+196)=2×46=92,
∴f(1)+f(2)+…+f(50)=f(1)+f(2)+f(3)+f(50)=288+188+92+92=660.
故答案为:660.
∴当4≤x≤49时,x2-53x+196≤0,
∴当4≤x≤49时,f(x)=x2-53x+196+|x2-53x+196|=x2-53x+196-(x2-53x+196)=0,
当x>49或x<4时,f(x)=x2-53x+196+|x2-53x+196|=x2-53x+196+(x2-53x+196)=2(x2-53x+196),
∴f(1)+f(2)+…+f(50)=f(1)+f(2)+f(3)+f(50)
∵f(1)=2(1-53+196)=2×144=288,
f(2)=2(4-53×2+196)=2×94=188,
f(3)=2(9-53×3+196)=2×46=92,
f(50)=2(502-53×50+196)=2×46=92,
∴f(1)+f(2)+…+f(50)=f(1)+f(2)+f(3)+f(50)=288+188+92+92=660.
故答案为:660.

练习册系列答案
相关题目
 在函数
在函数 的图象上,则
的图象上,则 的值为 .
的值为 .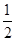 )-1.2,则a,b,c的大小关系为( )
)-1.2,则a,b,c的大小关系为( )