题目内容
8.已知函数f(x)=ln(1+x)(x>0).(Ⅰ)证明:$\frac{x}{1+x}<f(x)$;
(Ⅱ)比较20152013与20142014的大小;
(Ⅲ)给定正整数n(n>2015),n个正实数x1,x2,…,xn满足x1+x2+…+xn=1,
证明:${(\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_2}^2}}{{1+{x_2}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}})^{2015}}>{(\frac{1}{2016})^n}$.
分析 (Ⅰ)令$h(x)=f(x)-\frac{x}{1+x}=ln(1+x)-\frac{x}{1+x}(x>0)$,证明h(x)在(0,+∞)上是增函数,所以x>0时,h(x)>h(0)=0,即可证明结论;
(Ⅱ)令$g(x)=\frac{ln(1+x)}{x}(x>0)$,证明g(x)在(0,+∞)上是减函数,即可比较20152013与20142014的大小;
(Ⅲ)由x1+x2+…+xn=1及柯西不等式,证明$\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_1}^2}}{{1+{x_1}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}}≥\frac{1}{1+n}$,即可证明结论.
解答 (Ⅰ)证明:令$h(x)=f(x)-\frac{x}{1+x}=ln(1+x)-\frac{x}{1+x}(x>0)$,
则x>0时,$h'(x)=\frac{1}{1+x}-\frac{1}{{{{(1+x)}^2}}}=\frac{x}{{{{(1+x)}^2}}}>0$,
所以h(x)在(0,+∞)上是增函数,所以x>0时,h(x)>h(0)=0,
所以x>0时,$ln(1+x)>\frac{x}{1+x}$,即$\frac{x}{1+x}<f(x)$; …(4分)
(Ⅱ)解:令$g(x)=\frac{ln(1+x)}{x}(x>0)$,则$g'(x)=\frac{x-(1+x)ln(1+x)}{{{x^2}(1+x)}}$,
由(Ⅰ)知x>0时,x-(1+x)ln(1+x)<0,
所以x>0时,g'(x)<0,即g(x)在(0,+∞)上是减函数,
因为2014>2013,所以$\frac{ln(1+2014)}{2014}<\frac{ln(1+2013)}{2013}$,
即2013ln2015<2014ln2014,所以20152013<20142014; …(9分)
(Ⅲ)证明:由x1+x2+…+xn=1及柯西不等式得:$(\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_2}^2}}{{1+{x_2}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}})(1+n)$=$(\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_2}^2}}{{1+{x_2}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}})[(1+{x_1})+(1+{x_2})+…+(1+{x_n})]$$≥{(\sqrt{\frac{{{x_1}^2}}{{1+{x_1}}}}•\sqrt{1+{x_1}}+\sqrt{\frac{{{x_2}^2}}{{1+{x_2}}}}•\sqrt{1+{x_2}}+…+\sqrt{\frac{{{x_n}^2}}{{1+{x_n}}}}•\sqrt{1+{x_n}})^2}$=${({x_1}+{x_2}+…+{x_n})^2}=1$,
所以$\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_1}^2}}{{1+{x_1}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}}≥\frac{1}{1+n}$,
所以${(\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_1}^2}}{{1+{x_1}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}})^{2015}}≥{(\frac{1}{1+n})^{2015}}$,
又由(Ⅱ)知n>m>0时,$\frac{ln(1+n)}{n}<\frac{ln(1+m)}{m}$,因而(1+n)m<(1+m)n,
所以n>2015时,(1+n)2015<(1+2015)n,即(1+n)2015<2016n,
所以${(\frac{1}{1+n})^{2015}}>{(\frac{1}{2016})^n}$,
所以${(\frac{{{x_1}^2}}{{1+{x_1}}}+\frac{{{x_2}^2}}{{1+{x_2}}}+…+\frac{{{x_n}^2}}{{1+{x_n}}})^{2015}}>{(\frac{1}{2016})^n}$. …(14分)
点评 本题考查导数知识的综合运用,考查不等式的证明,考查学生分析解决问题的能力,难度大.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案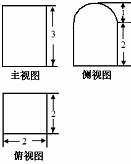
| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
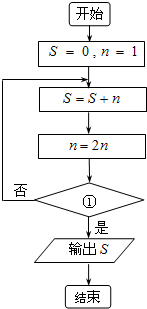
| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
| A. | -9 | B. | 9 | C. | -6 | D. | 3 |