题目内容
6.设复数$z=\frac{2}{-1-i}$,则$z•\overline z$=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
分析 首先化简复数z,然后矩形复数的运算.
解答 解:复数$z=\frac{2}{-1-i}$=$\frac{2(-1+i)}{(-1-i)(-1+i)}$=-1-i,
所以$z•\overline z$=(-1-i)(-1+i)=(-1)2-(i)2=1+1=2;
故选C.
点评 本题考查了复数的运算;注意i2=-1.属于基础题

练习册系列答案
相关题目
16.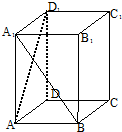 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.已知函数f(x)对定义域R内的任意x都有f(x)=f(4-x),且当x≠2时导函数满足xf′(x)>2f′(x),若2<a<4,则( )
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |
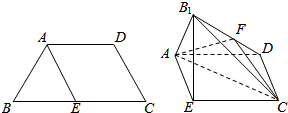 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.