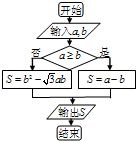
题目内容
1．
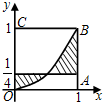如图，正方形OABC的边长为1，记曲线y=x2和直线$y=\frac{1}{4}$，x=1，x=0所围成的图形（阴影部分）为Ω，若向正方形OABC内任意投一点M，则点M落在区域Ω内的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{2}{5}$ |
分析 欲求所投的点落在阴影部分内部的概率，须结合定积分计算阴影部分平面区域的面积，再根据几何概型概率计算公式易求解
解答 解：根据题意，正方形OABC的面积为1×1=1，
而阴影部分的面积为${∫}_{0}^{\frac{1}{2}}（\frac{1}{4}-{x}^{2}）dx+{∫}_{\frac{1}{2}}^{1}（{x}^{2}-\frac{1}{4}）dx$=（$\frac{1}{4}x-\frac{1}{3}{x}^{3}$）|${\;}_{0}^{\frac{1}{2}}$+（$\frac{1}{3}{x}^{3}-\frac{1}{4}x$）|${\;}_{\frac{1}{2}}^{1}$=$\frac{1}{4}$，
由几何概型公式得到，向正方形OABC中任取一点M，点M取自阴影部分的概率$\frac{\frac{1}{4}}{1}=\frac{1}{4}$；
故选A．
点评 本题考查几何概型的计算，涉及定积分在求面积中的应用，关键是正确计算出阴影部分的面积．
练习册系列答案
相关题目
11．已知函数f（x）对定义域R内的任意x都有f（x）=f（4-x），且当x≠2时导函数满足xf′（x）＞2f′（x），若2＜a＜4，则（ ）
| A． | f（2a）＜f（3）＜f（log2a） | B． | f（3）＜f（log2a）＜f（2a） | C． | f（log2a）＜f（3）＜f（2a） | D． | f（log2a）＜f（2a）＜f（3） |
12．已知数列{an}为递增等比数列，其前n项和为Sn．若a1=1，2an+1+2an-1=5an（n≥2），则S5=（ ）
| A． | $\frac{31}{16}$ | B． | $\frac{31}{32}$ | C． | 31 | D． | 15 |
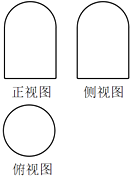一个几何体的三视图如图，正视图和侧视图都是由一个半圆和一个边长为2的正方形组成，俯视图是一个圆，则这个几何体的表面积为7π．