��Ŀ����
����Ŀ����ij��ҵ�����IJ�Ʒ�г�ȡ100��,������Щ��Ʒ��һ������ָ��ֵ,�ɲ������������Ƶ���ֲ���:
����ָ��ֵ���� | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
Ƶ�� | 6 | 26 | 38 | 22 | 8 |
��1���ڱ�����������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ;
��2������Щ���ݵ���������λ��
��3���������ֲ�Ʒ����ָ���ƽ����(ͬһ���е������ø���������е�ֵ������);
���𰸡���1�������������2������![]() ����λ��
�����![]() ����3��
����3��![]()
��������
��1������֪����Ƶ�ʷֲ������ɴ���������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
��2����Ƶ�ʷֲ�ֱ��ͼ���������ָ��ֵ��������������λ����
��3����Ƶ�ʷֲ�ֱ��ͼ���������ָ��ֵ������ƽ����.
��1������֪����Ƶ�ʷֲ���Ϊ��
����ָ��ֵ���� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��125�� |
Ƶ�� | 6 | 26 | 38 | 22 | 8 |
Ƶ�� | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
��Ƶ�ʷֲ���������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼΪ��
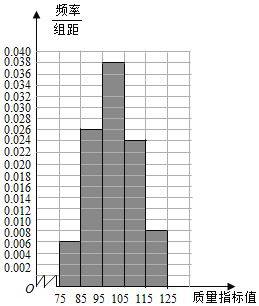
��2����С���θ߶���ߵ�λ������[95��105����������100��
��[75��95����Ƶ��Ϊ��0.06+0.26=0.32��
����λ��λ��[95��105���ڣ�
����λ��Ϊx����x=95+![]() ��99.7��
��99.7��
����λ��Ϊ99.7��
����100�����99.7
��3������ָ��ֵ������ƽ����Ϊ��![]() =80��0.06+90��0.26+100��0.38+110��0.22+120��0.08=100��
=80��0.06+90��0.26+100��0.38+110��0.22+120��0.08=100��

 ��У����ϵ�д�
��У����ϵ�д�