题目内容
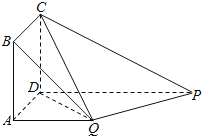
【题目】如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求直线DQ与面PQC成角的正弦值
【答案】(1)见解析 (2)![]()
【解析】
根据题意得以D为坐标原点,线段DA的长为单位长,射线DA,DP,DC分别为x,y,z轴建立空间直角坐标系D﹣xyz;(1)根据坐标系,求出![]() 的坐标,由向量积的运算易得
的坐标,由向量积的运算易得![]() =0,
=0, ![]() =0;进而可得PQ⊥DQ,PQ⊥DC,由面面垂直的判定方法,可得证明;(2)先求平面的PQC的法向量
=0;进而可得PQ⊥DQ,PQ⊥DC,由面面垂直的判定方法,可得证明;(2)先求平面的PQC的法向量![]() ,再求出cos<
,再求出cos<![]() ,
,![]() >,直线DQ与面PQC成角的正弦值等于cos<
>,直线DQ与面PQC成角的正弦值等于cos<![]() ,
,![]() >即可.
>即可.
如图,以D为坐标原点,线段DA的长为单位长,射线DA,DP,DC分别为x,y,z轴建立空间直角坐标系D﹣xyz;
(1)依题意有Q(1,1,0),C(0,0,1),P(0,2,0),D(0,0,0);
则![]() =(1,1,0),
=(1,1,0),![]() =(0,0,1),
=(0,0,1),![]() =(1,﹣1,0),
=(1,﹣1,0),
所以![]()
![]() =0,
=0,![]()
![]() =0;即PQ⊥DQ,PQ⊥DC,故PQ⊥平面DCQ,
=0;即PQ⊥DQ,PQ⊥DC,故PQ⊥平面DCQ,
又PQ平面PQC,所以平面PQC⊥平面DCQ;
(2)依题意,![]() =(1,﹣1,0),
=(1,﹣1,0),![]()
设![]() =(x,y,z)是平面的PQC法向量,
=(x,y,z)是平面的PQC法向量,
则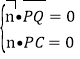 即
即![]() ,可取
,可取![]() =(1,1,2);
=(1,1,2);
![]() =(1,1,0),所以cos<
=(1,1,0),所以cos<![]() ,
,![]() >=
>=![]()
设直线DQ与面PQC所成的角为![]() ,
,
sin![]() =cos<
=cos<![]() ,
,![]() >=
>=![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案【题目】从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)在表格中作出这些数据的频率分布直方图;
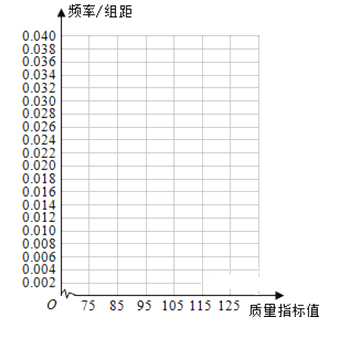
(2)求这些数据的众数和中位数
(3)估计这种产品质量指标的平均数(同一组中的数据用该组区间的中点值作代表);
【题目】随着苹果6手机的上市,很多消费者觉得价格偏高,尤其是一部分大学生可望而不可及,因此“国美在线”推出无抵押分期付款购买方式,某分期店对最近100位采用分期付款的购买者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频 数 | 35 | 25 | a | 10 | b |
已知分3期付款的频率为0.15,并且店销售一部苹果6,顾客分1期付款,其利润为1千元;分2期或3期付款,其利润为1.5千元;分4期或5期付款,其利润为2千元,以频率作为概率.
(1)求事件A:“购买的3位顾客中,至多有1位分4期付款”的概率;
(2)用X表示销售一该手机的利润,求X的分布列及数学期望E(x)
