题目内容
【题目】已知函数f（x）=x+ 
+b（x≠0），其中a，b∈R．若对任意的a∈[ 
，2]，不等式f（x）≤10在x∈[ 
，1]上恒成立，则b的取值范围为明 ．
【答案】（﹣∞， 
]
【解析】解：∵对任意的a∈[ 
，2]，不等式f（x）≤10在x∈[ 
，1]上恒成立，
∴当a= 时，f（x）最大值为f（1）=1+ +b= 
+b
当a=2时，f（x）最大值为f（ ）= +8+b= 
+b
显然 +b＞ +b，
∴ +b≤10，
∴b≤ ，
所以答案是：（﹣∞， ]
【考点精析】利用函数单调性的性质对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．
练习册系列答案
阅读快车系列答案
相关题目
【题目】从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
（1）在表格中作出这些数据的频率分布直方图;
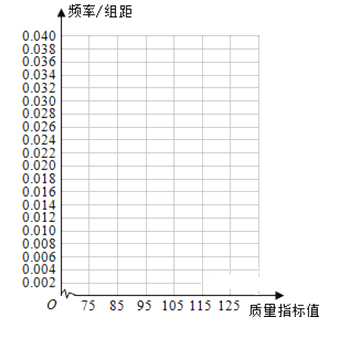
（2）求这些数据的众数和中位数
（3）估计这种产品质量指标的平均数(同一组中的数据用该组区间的中点值作代表);
