题目内容
【题目】设△ABC,P0是边AB上一定点,满足 ![]() ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有 ![]() 则( )
则( )
A.∠ABC=90°
B.∠BAC=90°
C.AB=AC
D.AC=BC
【答案】D
【解析】解:设| ![]() |=4,则|
|=4,则| ![]() |=1,过点C作AB的垂线,垂足为H ,
|=1,过点C作AB的垂线,垂足为H ,
在AB上任取一点P , 设HP0=a , 则由数量积的几何意义可得,![]() =|
=| ![]() ||
|| ![]() |=|
|=| ![]() |2﹣(a+1)|
|2﹣(a+1)| ![]() |,
|,![]()
![]() =﹣a ,
=﹣a ,
于是 ![]()
![]() ≥
≥ ![]()
![]() 恒成立,
恒成立,
整理得| ![]() |2﹣(a+1)|
|2﹣(a+1)| ![]() |+a≥0恒成立,
|+a≥0恒成立,
只需△=(a+1)2﹣4a=(a﹣1)2≤0即可,于是a=1,
因此我们得到HB=2,即H是AB的中点,故△ABC是等腰三角形,
所以AC=BC.
故选:D.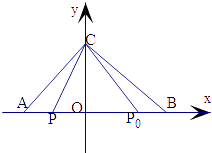

练习册系列答案
相关题目