Question

【题目】已知函数f（x）=sin（2ωx+）+sin（2ωx-）+2cos2ωx，其中ω＞0，且函数f（x）的最小正周期为π

（1）求ω的值；

（2）求f（x）的单调增区间

（3）若函数g（x）=f（x）-a在区间[-，]上有两个零点，求实数a的取值范围．

Answer 1

【答案】(1)1.(2) [-+kπ，+kπ]，k∈Z，(3)见解析.

【解析】

（1）利用三角函数恒等变换的应用化简函数解析式可得，利用三角函数周期公式可求的值．

（2）由正弦函数的单调性可求的单调增区间．

（3）作出函数在上的图象，从图象可看出 ，可求当曲线与在∈上有两个交点时，2，即可得解实数的取值范围．

（1）由三角恒等变换的公式，可得f（x）=sin（2+）+sin（2 -）+2

=sin2 +cos2 +sin2 -cos2 +1+cos2

=sin2 +cos2 +1，

又因为T==π，所以．

（2）由2kπ- 2+ 2kπ+，k∈Z，解得：-+kπ +kπ，k∈Z，

可得f（x）的单调增区间为：[-+kπ，+kπ]，k∈Z，

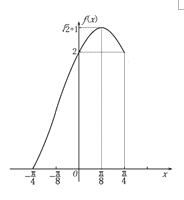
（3）作出函数在上的图象如图：

函数g（x）有两个零点，即方程有两解，

亦即曲线与在x∈上有两个交点，

从图象可看出f（0）=f（）=2，f（）=+1，

所以当曲线与在x∈上有两个交点时，

则2 ，即实数的取值范围是．