题目内容
【题目】如图，椭圆的中心为原点O，长轴在x轴上，离心率 
，过左焦点F1作x轴的垂线交椭圆于A、A′两点，|AA′|=4． 
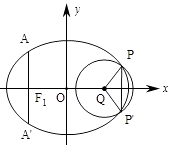
（1）求该椭圆的标准方程；
（2）取垂直于x轴的直线与椭圆相交于不同的两点P、P′，过P、P′作圆心为Q的圆，使椭圆上的其余点均在圆Q外．若PQ⊥P'Q，求圆Q的标准方程．
【答案】
（1）解：由题意知点A（﹣c，2）在椭圆上，则 
，即 
①
∵离心率 
，∴ 
②
联立①②得： 
，所以b2=8．
把b2=8代入②得，a2=16．
∴椭圆的标准方程为 
；
（2）解：设Q（t，0），圆Q的半径为r，则圆Q的方程为（x﹣t）2+y2=r2，
不妨取P为第一象限的点，因为PQ⊥P'Q，则P（ 
）（t＞0）．
联立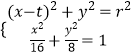 
，得x2﹣4tx+2t2+16﹣2r2=0．
由△=（﹣4t）2﹣4（2t2+16﹣2r2）=0，得t2+r2=8
又P（ ）在椭圆上，所以 
．
整理得， 
．
代入t2+r2=8，得 
．
解得： 
．所以 
， 
．
此时 
．
满足椭圆上的其余点均在圆Q外．
由对称性可知，当t＜0时，t=﹣ 
， ．
故所求圆Q的标准方程为 
【解析】（1）利用点A（﹣c，2）在椭圆上，结合椭圆的离心率，求出几何量，即可求得椭圆的标准方程；（2）设出圆Q的圆心坐标及半径，由PQ⊥P'Q得到P的坐标，写出圆的方程后和椭圆联立，化为关于x的二次方程后由判别式等于0得到关于t与r的方程，把P点坐标代入椭圆方程得到关于t与r的另一方程，联立可求出t与r的值，经验证满足椭圆上的其余点均在圆Q外，结合对称性即可求得圆Q的标准方程．
【题目】某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级．
（1）求一次摸奖恰好摸到1个红球的概率；
（2）求摸奖者在一次摸奖中获奖金额x的分布列与期望E（x）．
