题目内容
(本题15分)如图,椭圆 长轴端点为
长轴端点为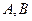 ,
,
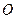 为椭圆中心,
为椭圆中心,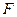 为椭圆的右焦点,且
为椭圆的右焦点,且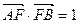
 ,
,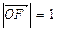 .(1)求椭圆的标准方程;(2)记椭圆的上顶点为
.(1)求椭圆的标准方程;(2)记椭圆的上顶点为 ,
, 直线
直线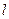 交椭圆于
交椭圆于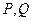 两点,问:是否存在直线
两点,问:是否存在直线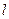 ,使点
,使点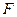 恰为
恰为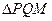 的垂心?若存在,求出
的垂心?若存在,求出 直线
直线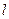 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.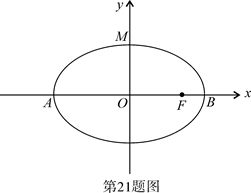
 长轴端点为
长轴端点为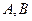 ,
,
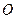 为椭圆中心,
为椭圆中心,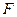 为椭圆的右焦点,且
为椭圆的右焦点,且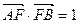
 ,
,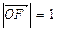 .(1)求椭圆的标准方程;(2)记椭圆的上顶点为
.(1)求椭圆的标准方程;(2)记椭圆的上顶点为 ,
, 直线
直线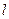 交椭圆于
交椭圆于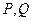 两点,问:是否存在直线
两点,问:是否存在直线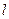 ,使点
,使点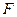 恰为
恰为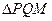 的垂心?若存在,求出
的垂心?若存在,求出 直线
直线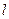 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(Ⅰ)
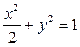 (Ⅱ)
(Ⅱ)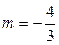
(1
 )如图建系,设椭圆方程为
)如图建系,设椭圆方程为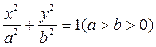 ,则
,则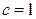
又∵
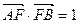 即
即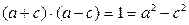
∴
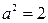
故
 椭圆方程为
椭圆方程为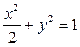 …………6分
…………6分(2)假设存在直线
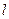 交椭圆于
交椭圆于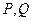 两点,且
两点,且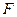
 恰
恰为
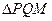 的垂心,则
的垂心,则

设
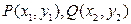 ,∵
,∵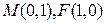 ,故
,故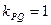 ,……8分
,……8分于是设直线

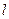 为
为 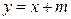 ,
, 由
由

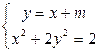 得
得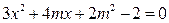 …10分
…10分∵
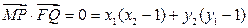 又
又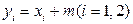
得
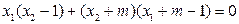 即
即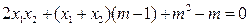 由韦达
由韦达 定理
定理 得
得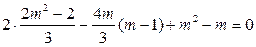
解得
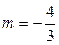 或
或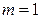
 (舍) 经
(舍) 经 检验
检验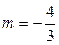 符合条件………15分
符合条件………15分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是椭圆
是椭圆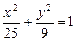 上的一点,
上的一点, 是椭圆的左焦点,且
是椭圆的左焦点,且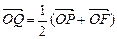 ,
,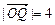 则点
则点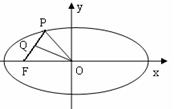
 .又AB的中点M与椭圆中心连线的斜率为
.又AB的中点M与椭圆中心连线的斜率为 ,求椭圆的方程.
,求椭圆的方程. ;②
;②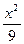 +
+ =1;?③x2+
=1;?③x2+ +y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )
+y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )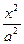 +
+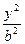 =1上取三点,其横坐标满足x1+x3=2x2,三点顺次与某一焦点连接的线段长是r1、r2、r3,则有( )
=1上取三点,其横坐标满足x1+x3=2x2,三点顺次与某一焦点连接的线段长是r1、r2、r3,则有( )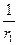 、
、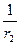 、
、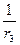 成等差数列
成等差数列 的椭圆方程是( )
的椭圆方程是( )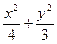 ="1"
="1"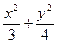 =1
=1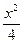 +y2="1"
+y2="1"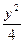 =1
=1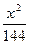 +
+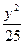 =1总有公共点,则b的取值范?围是( )
=1总有公共点,则b的取值范?围是( )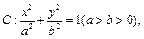 过点
过点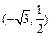 离心率
离心率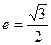 ,
,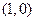 的直线
的直线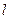 与椭圆C交于A、B两点,且以AB为直径的圆过原点,试求直线
与椭圆C交于A、B两点,且以AB为直径的圆过原点,试求直线