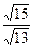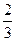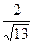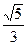题目内容
设椭圆ax2+by2=1与直线x+y=1相交于A、B两点,且|AB|=2 .又AB的中点M与椭圆中心连线的斜率为
.又AB的中点M与椭圆中心连线的斜率为 ,求椭圆的方程.
,求椭圆的方程.
 .又AB的中点M与椭圆中心连线的斜率为
.又AB的中点M与椭圆中心连线的斜率为 ,求椭圆的方程.
,求椭圆的方程.椭圆方程为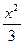 +
+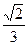 y2=1.
y2=1.
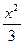 +
+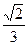 y2=1.
y2=1.将椭圆方程与直线方程联立,消去y并整理得(a+b)x2-2bx+b-1=0.
设A(x1,y1)、B(x2,y2),
则x1+x2=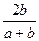 ,x1x2=
,x1x2= .
.
∴|AB|=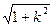 |x1-x2|
|x1-x2|
=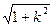 ·
·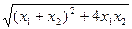
=2·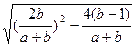
=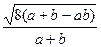 ,
,
y1+y2=1-x1+1-x2=2-(x1+x2)=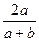 ,kOM=
,kOM=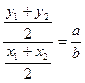 .
.
由题意知
解之,得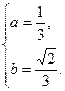
故所求椭圆方程为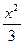 +
+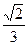 y2=1.
y2=1.
设A(x1,y1)、B(x2,y2),
则x1+x2=
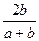 ,x1x2=
,x1x2= .
.∴|AB|=
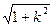 |x1-x2|
|x1-x2|=
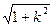 ·
·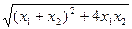
=2·
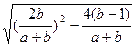
=
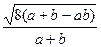 ,
,y1+y2=1-x1+1-x2=2-(x1+x2)=
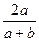 ,kOM=
,kOM=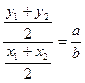 .
.由题意知

解之,得
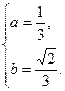
故所求椭圆方程为
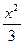 +
+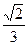 y2=1.
y2=1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
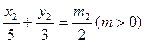 ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.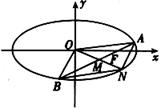
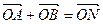 成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;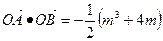 ,求实数k的取值范围.
,求实数k的取值范围. 经过点
经过点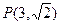 ,且与
,且与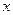 轴交于
轴交于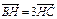 .
.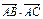 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;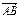 的比为
的比为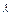 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤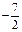 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.
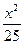 +
+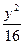 =1上一点,则
=1上一点,则 x+
x+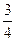 y的最小值为__________________.
y的最小值为__________________.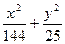 =1有两个公共点,则m的取值范围是( )
=1有两个公共点,则m的取值范围是( ) 长轴端点为
长轴端点为 ,
,
 为椭圆中心,
为椭圆中心,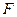 为椭圆的右焦点,且
为椭圆的右焦点,且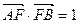
 ,
,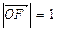 .(1)求椭圆的标准方程;(2)记椭圆的上顶点为
.(1)求椭圆的标准方程;(2)记椭圆的上顶点为 ,
, 直线
直线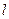 交椭圆于
交椭圆于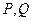 两点,问:是否存在直线
两点,问:是否存在直线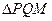 的垂心?若存在,求出
的垂心?若存在,求出 直线
直线
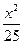 +
+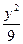 =1上点P到右焦点的距离…( )
=1上点P到右焦点的距离…( )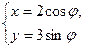 (φ为参数)的离心率为( )
(φ为参数)的离心率为( )