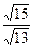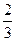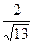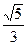题目内容
给定四条曲线:①x2+y2= ;②
;②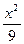 +
+ =1;?③x2+
=1;?③x2+ =1;④
=1;④ +y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )
+y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )
 ;②
;②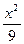 +
+ =1;?③x2+
=1;?③x2+ =1;④
=1;④ +y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )
+y2=1.其中与直线x+y-5=0仅有一个交点的曲线是( )| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
D
将y=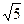 -x分别代入四条曲线的方程:
-x分别代入四条曲线的方程:
代入①,得4x2-4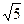 x+5=0,Δ=0;
x+5=0,Δ=0;
代入②,得13x2-18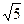 x+9=0,Δ>0;
x+9=0,Δ>0;
代入③,得5x2-2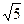 x+1=0,Δ=0;
x+1=0,Δ=0;
代入④,得5x2-8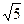 x+16=0,Δ=0.
x+16=0,Δ=0.
∴①③④仅与x+y-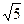 =0有一个交点.
=0有一个交点.
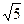 -x分别代入四条曲线的方程:
-x分别代入四条曲线的方程:代入①,得4x2-4
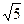 x+5=0,Δ=0;
x+5=0,Δ=0;代入②,得13x2-18
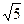 x+9=0,Δ>0;
x+9=0,Δ>0;代入③,得5x2-2
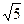 x+1=0,Δ=0;
x+1=0,Δ=0;代入④,得5x2-8
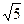 x+16=0,Δ=0.
x+16=0,Δ=0.∴①③④仅与x+y-
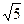 =0有一个交点.
=0有一个交点.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 中,已知椭圆
中,已知椭圆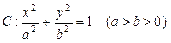 的离心率e=
的离心率e=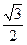 ,左右两个焦分别为
,左右两个焦分别为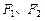 .过右焦点
.过右焦点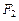 且与
且与 轴垂直的
轴垂直的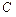 相交M、N两点,且|MN|=1.
相交M、N两点,且|MN|=1.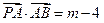 ,
,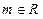 )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆
)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆
 .
. = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;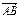 的比为
的比为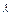 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤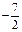 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.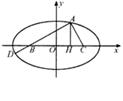
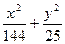 =1有两个公共点,则m的取值范围是( )
=1有两个公共点,则m的取值范围是( )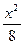 +
+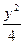 =1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________.
=1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________. 长轴端点为
长轴端点为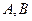 ,
,
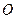 为椭圆中心,
为椭圆中心,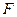 为椭圆的右焦点,且
为椭圆的右焦点,且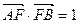
 ,
,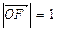 .(1)求椭圆的标准方程;(2)记椭圆的上顶点为
.(1)求椭圆的标准方程;(2)记椭圆的上顶点为 ,
, 直线
直线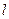 交椭圆于
交椭圆于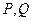 两点,问:是否存在直线
两点,问:是否存在直线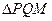 的垂心?若存在,求出
的垂心?若存在,求出 直线
直线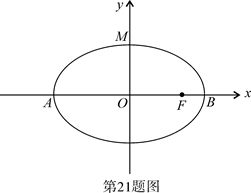
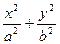 =1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.
=1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.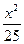 +
+ =1和椭圆C2:
=1和椭圆C2: +
+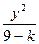 =1有( )
=1有( )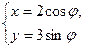 (φ为参数)的离心率为( )
(φ为参数)的离心率为( )