题目内容
10.如图所示,直线y=kx分抛物线y=x2-x与x轴所围成图形为面积相等的两部分,则实数k的值为$\frac{\root{3}{4}}{2}-1$.
分析 由题意得到${∫}_{0}^{1}(x-{x}^{2})dx$=2${∫}_{0}^{k+1}(kx-{x}^{2}+x)dx$整理得到关于k的等式解之.
解答 解:由题意由$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-x}\end{array}\right.$得到交点为(0,0),(k+1,k(k+1)),
所以${∫}_{0}^{1}(x-{x}^{2})dx$=2${∫}_{0}^{k+1}(kx-{x}^{2}+x)dx$
整理得($\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=2($\frac{k}{2}{x}^{2}-\frac{1}{3}{x}^{3}+\frac{1}{2}{x}^{2}$)|${\;}_{0}^{k+1}$
所以(k+1)3=$\frac{1}{2}$,解得k=$\frac{\root{3}{4}}{2}-1$;
故答案为:$\frac{{\root{3}{4}}}{2}-1$
点评 本题考查了运用定积分求曲边梯形的面积;关键是利用定积分表示出面积的关系.

练习册系列答案
相关题目
1.扇形周长为6cm,面积为2cm2,则其中心角的弧度数是( )
| A. | 1或4 | B. | 1或2 | C. | 2或4 | D. | 1或5 |
16.袋中装有6只白球,5只黄球,4只红球,从中任取一球,抽到不是白球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{15}$ | C. | $\frac{3}{5}$ | D. | .非以上答案 |
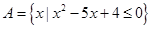 ,集合
,集合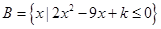 .
.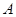 ;
;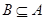 ,求实数
,求实数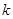 的取值范围.
的取值范围.