��Ŀ����
7��������ΪR�ĺ���f��x��=$\left\{{\begin{array}{l}{\frac{1}{|x-1|}��x��1}\\{1��x=1}\end{array}}$��������h��x��=f2��x��+bf��x��+$\frac{1}{3}$�������ͬ�����x1��x2��x3��x4��x5����x12+x22+x32+x42+x52��ֵΪ��������| A�� | $\frac{{2{b^2}+2}}{b^2}$ | B�� | 16 | C�� | 25 | D�� | 15 |
���� ���ݺ���f��x���ı���ʽ�ɶ�x��x=1��x��1���ۣ��ɷ���f2��x��+bf��x��+$\frac{1}{3}$=0�ֱ����x1��x2��x3��x4��x5���Ӷ��������x12+x22+x32+x42+x52��ֵ��
��� �⣺����x=1��f��x��=1����12+b+$\frac{1}{3}$=0��b=-$\frac{4}{3}$��
����x��1��f��x��=$\frac{1}{|x-1|}$������f2��x��+bf��x��+$\frac{1}{3}$=0�ɻ�Ϊ��$\frac{1}{|x-1|}$-1��•��$\frac{1}{|x-1|}$-$\frac{1}{3}$��=0��
��$\frac{1}{|x-1|}$=1��$\frac{1}{|x-1|}$=$\frac{1}{3}$��
��$\frac{1}{|x-1|}$=1�ã�x=0��x=2����$\frac{1}{|x-1|}$=$\frac{1}{3}$�ã�x=-2��x=4��
��x12+x22+x32+x42+x52=12+02+22+��-2��2+42=25��
��ѡ��C��
���� ���⿼����Ĵ����Լ����ĸ����жϣ��ؼ���ͨ����x��x=1��x��1���ۣ��ɷ���f2��x��+bf��x��+$\frac{1}{3}$=0�ֱ����x1��x2��x3��x4��x5��

��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ
15������P��1��1����ֱ�߱�Բx2+y2=4�صõ���ȡ����Сֵ�����ֱ�ߵķ���Ϊ��������
| A�� | x+y-2=0 | B�� | y-1=0 | C�� | x-y=0 | D�� | x+3y-4=0 |
19������+��=$\frac{��}{4}$����tan��+1��•��tan��+1��=��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 6 |
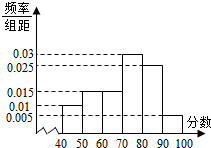 �Ӳμӻ���������ѧ���г��60��������ɼ�����Ϊ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣺
�Ӳμӻ���������ѧ���г��60��������ɼ�����Ϊ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣺