题目内容
15．过点P（1，1）的直线被圆x2+y2=4截得的弦取得最小值，则该直线的方程为（ ）| A． | x+y-2=0 | B． | y-1=0 | C． | x-y=0 | D． | x+3y-4=0 |
分析 过点P的直线中，被圆截得的弦长最短时，弦心距最大，故当且仅当与OP垂直时，弦长最短，求出直线的斜率，即可得到直线的方程．
解答 解：过点P的直线中，被圆截得的弦长最短时，弦心距最大，故当且仅当与OP垂直时，弦长最短，
∵OP的斜率为1，
∴所求直线的斜率为-1，
∴所求直线的方程为y-1=-（x-1），即x+y-2=0，
故选：A．
点评 本题考查直线和圆的方程的运用，考查弦长问题，解题的关键是得到过点P的直线中，被圆截得的弦长最短时，弦心距最大．
练习册系列答案
相关题目
6．已知实数x，y满足2x+2y=1，则x+y的最大值是（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 2 |
3．在△ABC中，b=4，c=7，A=60°，则a的值是（ ）
| A． | 6 | B． | $\sqrt{37}$ | C． | $\sqrt{38}$ | D． | $\sqrt{39}$ |
10．
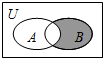设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）
设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）| A． | {x|0≤x＜1} | B． | {x|0≤x≤1} | C． | {x|1＜x＜2} | D． | {x|1＜x≤2} |
7．定义域为R的函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{|x-1|}，x≠1}\\{1，x=1}\end{array}}$，若函数h（x）=f2（x）+bf（x）+$\frac{1}{3}$有五个不同的零点x1，x2，x3，x4，x5，则x12+x22+x32+x42+x52的值为（ ）
| A． | $\frac{{2{b^2}+2}}{b^2}$ | B． | 16 | C． | 25 | D． | 15 |
5．已知函数y=logax（a＞0，a≠1）的图象经过点（4，$\frac{1}{2}$），则a的值为（ ）
| A． | 16 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |