题目内容
18．已知△ABC中，AB=$\sqrt{3}$，BC=1，A=30°，则AC=1或2．分析 由已知数据和余弦定理可得AC的方程，解方程可得．
解答 解：∵△ABC中，AB=$\sqrt{3}$，BC=1，A=30°，
∴由余弦定理可得BC2=AB2+AC2-2ABACcosA，
代入数据可得1=3+AC2-2$\sqrt{3}$AC•$\frac{\sqrt{3}}{2}$，
∴AC2-3AC+2=0，
∴（AC-1）（AC-2）=0，
解得AC=1或AC=2
故答案为：1或2
点评 本题考查余弦定理，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
9．将函数y=sin（2x+φ）的图象沿x轴向左平移$\frac{π}{8}$个单位后，得到函数f（x）的图象，且满足f（x）=f（-x），则φ的一个可能取值为（ ）
| A． | $\frac{3π}{4}$ | B． | $\frac{π}{4}$ | C． | 0 | D． | -$\frac{π}{4}$ |
6．已知实数x，y满足2x+2y=1，则x+y的最大值是（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 2 |
13．已知$\overrightarrow a=（1，2）$，$\overrightarrow b=（2x，-3）$且$\overrightarrow a∥\overrightarrow b$，则x=（ ）
| A． | -3 | B． | -$\frac{3}{4}$ | C． | 0 | D． | $\frac{3}{4}$ |
3．在△ABC中，b=4，c=7，A=60°，则a的值是（ ）
| A． | 6 | B． | $\sqrt{37}$ | C． | $\sqrt{38}$ | D． | $\sqrt{39}$ |
10．
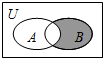设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）
设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）| A． | {x|0≤x＜1} | B． | {x|0≤x≤1} | C． | {x|1＜x＜2} | D． | {x|1＜x≤2} |