若α+β=$\frac{π}{4}$.则•A．1B．2C．3D．6 题目和参考答案——青夏教育精英家教网—

题目内容

19．若α+β=$\frac{π}{4}$，则（tanα+1）•（tanβ+1）=（　　）

A．

B．

C．

D．

分析根据条件和两角和的正切函数的变形化简已知的值，再由特殊角的正切值求值即可．

解答解：由题意知，α+β=$\frac{π}{4}$，
则（tanα+1）•（tanβ+1）=tanα•tanβ+tanα+tanβ+1
=tan（α+β）（1-tanα•tanβ）+tanα•tanβ+1
=tan$\frac{π}{4}$•（1-tanα•tanβ）+tanα•tanβ+1
=2，
故选：B．

点评本题考查两角和的正切函数的变形的应用，属于基础题．

练习册系列答案

10．

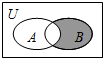设全集U是实数集R，集合A={y|y=3^x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（　　）

7．定义域为R的函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{|x-1|}，x≠1}\\{1，x=1}\end{array}}$，若函数h（x）=f²（x）+bf（x）+$\frac{1}{3}$有五个不同的零点x₁，x₂，x₃，x₄，x₅，则x₁²+x₂²+x₃²+x₄²+x₅²的值为（　　）

A．

$\frac{{2{b^2}+2}}{b^2}$

B．

C．

D．

14．已知已知角α的终边过点A（-3，1），求下列各式的值．
（1）$\frac{sinα+2cosα}{5cosα-sinα}$；
（2）$\frac{1}{{2sinαcosα+{{cos}^2}α}}$．

4．若不等式ax²-bx+c＜0的解集是（-2，3），则不等式bx²+ax+c＜0的解集是（-3，2）．

11．某同学在电脑上设置一个游戏，他让一弹性球从100m高出下落，每次着地后又跳回原来的高度的一半再落下，则第8次着地时所经过的路程和为（　　）

8．设a＞0，若${（{1+a\sqrt{x}}）^n}$的展开式中含x²项的系数等于含x项的系数的9倍，且展开式第3项等于135x，则a=3．

9．设等差数列{a_n}的各项均为整数，其公差d≠0，a₅=6，若无穷数列a₃，a₅，a${\;}_{{n}_{1}}$，a${\;}_{{n}_{2}}$，…，a${\;}_{{n}_{t}}$，…（5＜n₁＜n₂＜…＜n_t＜…）构成等比数列，则数列{a_n}的前2015项中是该等比数列中项的个数为7．

试题分类