题目内容
2．一质点按规律s=2t3运动，则其在时间段[1，1.1]内的平均速度为6.62m/s，在t=1时的瞬时速度为62m/s．分析 根据平均速度的求解公式平均速度=位移÷时间，建立等式关系即可，利用导数的物理意义即可得出．
解答 解：$\overline{v}$=$\frac{s（1.1）-s（1）}{1.1-1}$=$\frac{2×1．{1}^{3}-2×{1}^{3}}{0.1}$=6.62．
v（t）=s′=6t2，
把t=1代入可得t=1时的瞬时速度为v（1）=s′=6，
故答案为：6.62，6．
点评 本题考查了导数的物理意义，本题主要考查了函数的平均变化率公式，注意平均速度与瞬时速度的区别，属于基础题．
练习册系列答案
相关题目
13．已知$\overrightarrow a=（1，2）$，$\overrightarrow b=（2x，-3）$且$\overrightarrow a∥\overrightarrow b$，则x=（ ）
| A． | -3 | B． | -$\frac{3}{4}$ | C． | 0 | D． | $\frac{3}{4}$ |
10．
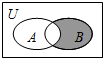设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）
设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=$\sqrt{2x-{x}^{2}}$}，则图中阴影部分所表示的集合是（ ）| A． | {x|0≤x＜1} | B． | {x|0≤x≤1} | C． | {x|1＜x＜2} | D． | {x|1＜x≤2} |
17．若直线l的斜率$k=-\frac{{\sqrt{3}}}{3}$，则其倾斜角为（ ）
| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
7．定义域为R的函数f（x）=$\left\{{\begin{array}{l}{\frac{1}{|x-1|}，x≠1}\\{1，x=1}\end{array}}$，若函数h（x）=f2（x）+bf（x）+$\frac{1}{3}$有五个不同的零点x1，x2，x3，x4，x5，则x12+x22+x32+x42+x52的值为（ ）
| A． | $\frac{{2{b^2}+2}}{b^2}$ | B． | 16 | C． | 25 | D． | 15 |
11．某同学在电脑上设置一个游戏，他让一弹性球从100m高出下落，每次着地后又跳回原来的高度的一半再落下，则第8次着地时所经过的路程和为（ ）
| A． | 99.8 m | B． | 198.4m | C． | 298.4m | D． | 266.9m |