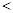题目内容
设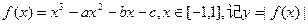 的最大值为M。
的最大值为M。
(1)当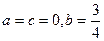 时,求M的值。
时,求M的值。
(2)当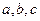 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值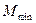 ;
;
(以下结论可供参考:对于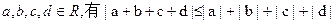 ,当
,当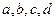 同号时取等号)
同号时取等号)
(3)对于第(2)小题中的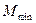 ,设数列
,设数列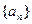 满足
满足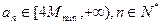 ,求证:
,求证: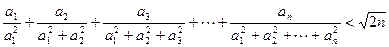 。
。
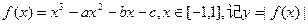 的最大值为M。
的最大值为M。(1)当
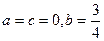 时,求M的值。
时,求M的值。(2)当
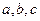 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值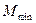 ;
;(以下结论可供参考:对于
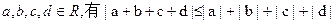 ,当
,当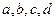 同号时取等号)
同号时取等号)(3)对于第(2)小题中的
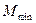 ,设数列
,设数列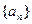 满足
满足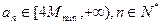 ,求证:
,求证: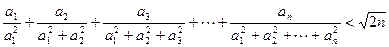 。
。(1)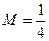 (2)
(2) 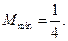 (3)见解析
(3)见解析
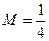 (2)
(2) 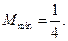 (3)见解析
(3)见解析(1)求导可得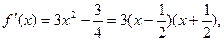
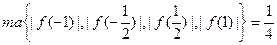
当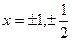 时取等号 3分
时取等号 3分
(2)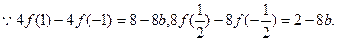
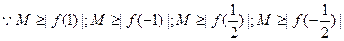 5分
5分
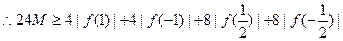
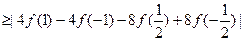 =6,
=6,
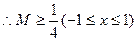 。
。
由(1)可知,当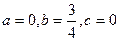 时,
时, 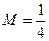 。
。
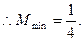 7分
7分
(3)证法一:(局部放缩法)因为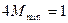 ,
,
所以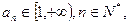
由于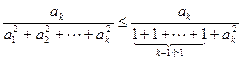
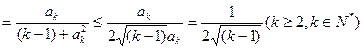 9分
9分
所以不等式左边
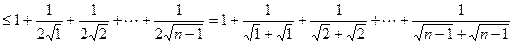
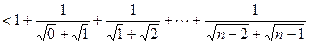
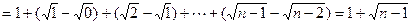 11分
11分
下证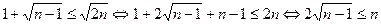
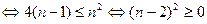 ,
,
显然。即证。 12分
证法二:(数学归纳法)即证:当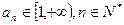
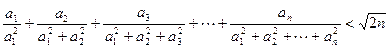
下用数学归纳法证明:
①当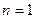 时,左边
时,左边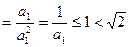 ,显然;
,显然;
②假设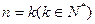 时命题成立,即
时命题成立,即
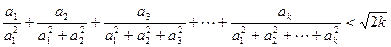 8分
8分
当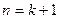 时,
时,
左边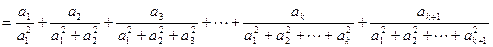
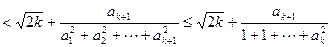 (
(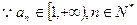 )
)
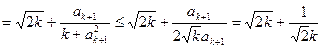 11分
11分
下证: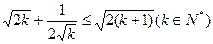 (*)
(*)
(*)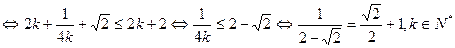 ,
,
显然。
所以命题对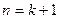 时成立。
时成立。
综上①②知不等式对一切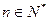 成立。 12分
成立。 12分
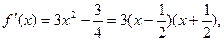
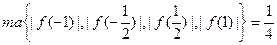
当
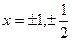 时取等号 3分
时取等号 3分(2)
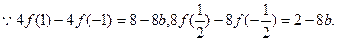
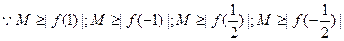 5分
5分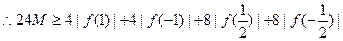
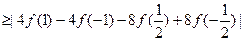 =6,
=6,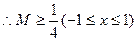 。
。由(1)可知,当
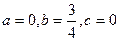 时,
时, 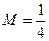 。
。 7分
7分(3)证法一:(局部放缩法)因为
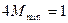 ,
,所以
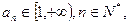
由于
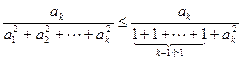
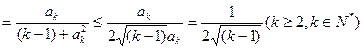 9分
9分所以不等式左边
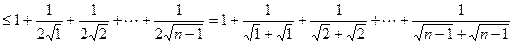
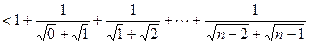
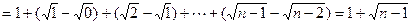 11分
11分下证
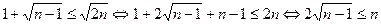
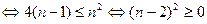 ,
,显然。即证。 12分
证法二:(数学归纳法)即证:当
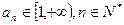
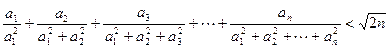
下用数学归纳法证明:
①当
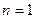 时,左边
时,左边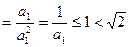 ,显然;
,显然;②假设
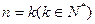 时命题成立,即
时命题成立,即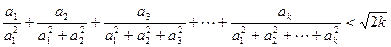 8分
8分当
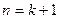 时,
时,左边
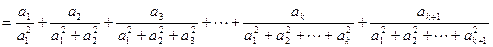
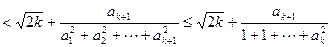 (
(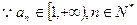 )
)
|
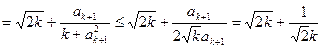 11分
11分下证:
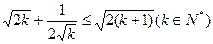 (*)
(*) (*)
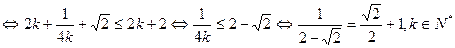 ,
,显然。
所以命题对
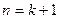 时成立。
时成立。综上①②知不等式对一切
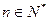 成立。 12分
成立。 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
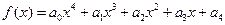 ,
,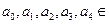 R. 当
R. 当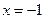 时,
时,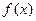 取得极大值
取得极大值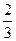 ,且函数
,且函数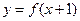 的图象关于点
的图象关于点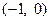 对称.
对称.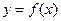 的表达式;
的表达式;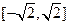 上,并说明理由;
上,并说明理由; (III)设
(III)设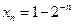 ,
,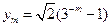 (
(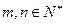 ),求证:
),求证: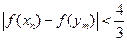 .
.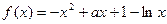 .
.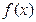 在
在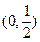 上是减函数,求
上是减函数,求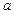 的取值范围;
的取值范围;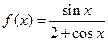 。
。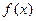 的单调区间;
的单调区间;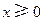 ,都有
,都有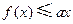 ,求
,求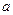 的取值范围。
的取值范围。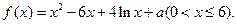 (1)求函数的单调区间;(2)
(1)求函数的单调区间;(2)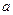 为何值时,方程
为何值时,方程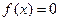 有三个不同的实根.
有三个不同的实根.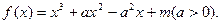
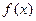 在
在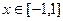 内没有极值点,求
内没有极值点,求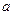 的取值范围。
的取值范围。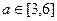 ,不等式
,不等式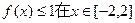 上恒成立,求实数
上恒成立,求实数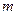 的取值范围。
的取值范围。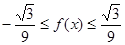 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。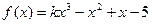 在R上单调递增,记
在R上单调递增,记 的三内角
的三内角 的对应边分别为
的对应边分别为 ,若
,若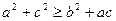 时,不等式
时,不等式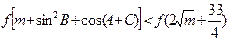 恒成立.
恒成立.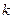 的取值范围;
的取值范围;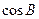 的取值范围;
的取值范围;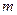 的取值范围.
的取值范围.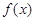 (
(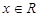 )满足
)满足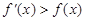 ,则当
,则当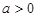 时,
时,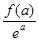 和
和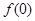 的大小关系为
的大小关系为