题目内容
1.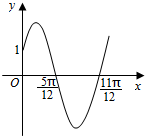 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)求函数g(x)=f($\frac{x}{2}$-$\frac{π}{12}$)•f($\frac{x}{2}$+$\frac{π}{12}$)的单调递增区间.
分析 (1)根据三角函数的图象求出A,ω和φ的值即可求函数f(x)的解析式;
(2)求出g(x)的表达式,利用三角函数的单调性即可求出单调递增区间.
解答 解:(1)由图象知函数的周期T=2($\frac{11π}{12}-\frac{5π}{12}$)=π,
即ω=$\frac{2π}{T}=\frac{2π}{π}$=2,
则f(x)=Asin(2x+φ),
∵0<φ<$\frac{π}{2}$,
∴由五点对应法知2×$\frac{5π}{12}$+φ=π,
解得φ=$\frac{π}{6}$,即f(x)=Asin(2x+$\frac{π}{6}$),
∵f(0)=Asin$\frac{π}{6}$=$\frac{1}{2}A$=1,
∴A=2,
即函数f(x)的解析式f(x)=2sin(2x+$\frac{π}{6}$);
(2)g(x)=f($\frac{x}{2}$-$\frac{π}{12}$)•f($\frac{x}{2}$+$\frac{π}{12}$)=2sin(x-$\frac{π}{6}$+$\frac{π}{6}$)•2sin(x+$\frac{π}{6}$+$\frac{π}{6}$)=4sinxsin(x+$\frac{π}{3}$)
=4sinx($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)=2sin2x+2$\sqrt{3}$sinxcosx=1-cos2x+$\sqrt{3}$sin2x=2sin(2x-$\frac{π}{6}$)+1,
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
即g(x)的单调递增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
点评 本题主要考查三角函数的图象和性质,根据图象求出A,ω和φ的值是解决本题的关键.综合考查三角函数的性质.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 3 | B. | -3 | C. | ±3 | D. | 5 |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分且必要 | D. | 既不充分也不必要 |
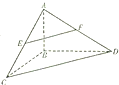 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点