题目内容
9.命题p:已知f(x)=x2+(m2-1)x+(m-2)的一个零点比1大,一个零点比1小.命题q:$\frac{1}{{m}^{2}}$-4m2≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1在x∈[$\frac{3}{2}$,+∞)上恒成立.
若¬p为假命题,p∧q为真命题,求m的取值范围.
分析 若¬p为假命题,p∧q为真命题,则p,q同时为真命题,然后分别求出p,q为真命题的等价条件即可
解答 解:∵¬p为假命题,p∧q为真命题,
∴p为真,q为真,
命题p,设方程的两根分别为x1,x2,且x1<x2,则(x1-1)(x2-1)<0,x1,•x2-(x1+x2)+1<0,
由根与系数的关系得:(m-2)+(m2-1)+1<0,即-2<m<1,
命题q:$\frac{1}{{m}^{2}}$-4m2≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1在x∈[$\frac{3}{2}$,+∞)上恒成立,
当x=$\frac{3}{2}$时,函数y=≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1取得最小值-$\frac{5}{3}$,
∴$\frac{1}{{m}^{2}}$-4m2≤-$\frac{5}{3}$,
解得m≤-$\frac{\sqrt{3}}{2}$,或m≥$\frac{\sqrt{3}}{2}$,
综上所述-2<m≤-$\frac{\sqrt{3}}{2}$,或$\frac{\sqrt{3}}{2}$≤m<1.
点评 本题主要考查复合命题的应用,要求熟练掌握复合命题与简单命题的真假关系,以及函数恒成立的问题,和一元二次方程根的关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |
14.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
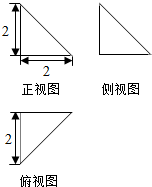

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
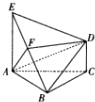 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.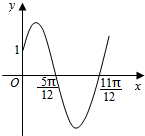 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.