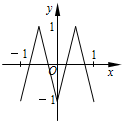题目内容
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为1.6,两焦点的距离为3,则a+b=$\frac{15}{16}$+$\frac{3\sqrt{39}}{16}$.分析 双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为1.6,两焦点的距离为3,求出a,c,可得b,即可得出结论.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为1.6,两焦点的距离为3,
∴$\frac{c}{a}$=1.6,c=1.5,
∴a=$\frac{15}{16}$,b=$\frac{3\sqrt{39}}{16}$,
∴a+b=$\frac{15}{16}$+$\frac{3\sqrt{39}}{16}$.
故答案为:$\frac{15}{16}$+$\frac{3\sqrt{39}}{16}$.
点评 本题考查双曲线的几何性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
3.已知正项等比数列{an}满足a7=a6+2a5,若am,an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
1.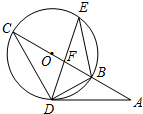 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
下列结论中,错误的是( )
 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的下列结论中,错误的是( )
| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
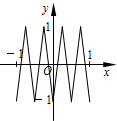
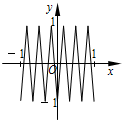
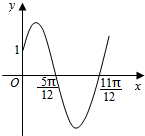 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.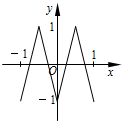 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=f[fn(x)],n∈N*,则函数y=f4(x)的图象为( )