题目内容
12.已知角α的终边经过点P(-b,4)且cosα=-$\frac{3}{5}$,则b的值等于( )| A. | 3 | B. | -3 | C. | ±3 | D. | 5 |
分析 根据三角函数的定义建立方程关系即可.
解答 解:∵角α的终边经过点P(-b,4)且cosα=-$\frac{3}{5}$,
∴cosα=$\frac{-b}{\sqrt{16+{b}^{2}}}$=-$\frac{3}{5}$,
则b>0,
平方得$\frac{{b}^{2}}{16+{b}^{2}}=\frac{9}{25}$,
即b2=9,解得b=3或b=-3(舍),
故选:A
点评 本题主要考查三角函数的定义的应用,注意求出的b为正值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.如图所示,程序框图(算法流程图)的输出结果为( )
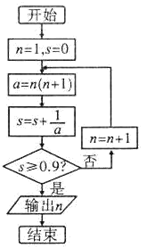

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
3. 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )| A. | 甲 | B. | 乙 | C. | 甲、乙相等 | D. | 无法确定 |
7.已知F1、F2为椭圆的两个焦点,以线段F1F2为一边的正方形ABF2F1与椭圆交于M,N两点,且M,N分别为边AF1,BF2的中点,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |
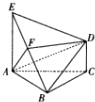 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.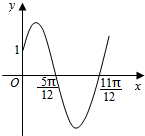 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.